Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 16:
Nếu giống ở bài thì phải là \(AB=3cm,CD=5cm\) nhé.
Cách dựng:
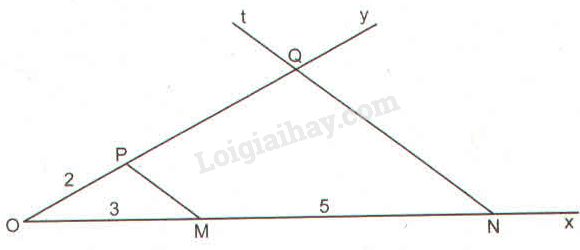
- Dựng hai tia chung gốc \(Ox\) và \(Oy\) phân biệt không đối nhau.
- Trên \(Ox\) dựng đoạn \(OM=AB=3cm\) và dựng đoạn \(MN=CD=5cm\) sao cho M nằm giữa O và N.
- Trên tia \(Oy\) dựng đoạn \(OP=EF=2cm.\)
- Dựng đường thẳng \(PM.\)
- Từ N dựng đường thẳng song song với \(PM\) cắt tia \(Oy\) tại Q. Ta được đoạn thẳng \(PQ=a\) cần dựng.
Chứng minh:
+ Xét \(\Delta ONQ\) có:
\(PM\) // \(NQ\) (do cách dựng).
=> \(\frac{OM}{MN}=\frac{OP}{PQ}\) (định lí Ta - lét).
=> \(\frac{AB}{CD}=\frac{EF}{a}\)
=> \(\frac{3}{5}=\frac{2}{a}\)
=> \(a=2:\frac{3}{5}\)
=> \(a=\frac{10}{3}\left(cm\right).\)
Vậy \(a=\frac{10}{3}\left(cm\right).\)
Chúc bạn học tốt!

a ) Ta có :
Góc BAD + ADC = 180o
=> \(\frac{1}{2}gocBAD+\frac{1}{2}gocADC=\frac{1}{2}.180^o\)
=> \(gocMAD+gocMDA=90^o\)
=> Xét \(\Delta MAD\)có \(gocMAD+gocMDA=90^o\Rightarrow gocAMD=90^o\)
=> Sử dụng góc kề bù ta suy ra \(gocAMD=gocAMF=gocDME=90^o\)
Xét \(\Delta AMD=\Delta AMF\left(g.c.g\right)\)
\(gocDAM=gocFAM\)( AE là phân giác góc A )
Chung cạnh AM
\(gocAMD=gocAMF\left(cmt\right)\)
=> \(\Delta AMD=\Delta AMF\left(g.c.g\right)\)
=> M là trung điểm DF
Tớ chỉ làm được tới đây

E là TĐ của MQ, F là TĐ của NP
=> EF là đ trung bình của hình thang MNPQ
=> EF//MN
hay ED//MN
mà E là TĐ của MQ
=> D là TĐ của QN
=> ED là đ trung bình của Δ MQN
=> ED=1/2MN(1)
Tương tự: BF=1/2MN(2)
Từ 1 và 2 => ED=BF
=> ED + DB=BF+DB => EB=FD
b,do EF là đ trung bình của hình thang MNPQ
=>\(EF=\dfrac{MN+PQ}{2}\)= \(\dfrac{3+5}{2}\)=4(cm) (3)
Do ED=BF=1/2MN
=> ED=BF=\(\dfrac{3}{2}\)(cm) (4)
Từ 3 và 4 => BD= EF-ED-BF=1(cm)

* Cách dựng:
- Dựng hai tia chung gốc ox và Oy
phân biệt không đối nhau.
- Trên Ox dựng đoạn OM = AB = 3cm
và dựng đoạn MN = CD = 5cm sao cho M nằm giữa O và N
- Trên tia Oy dựng đoạn OP = EF = 2cm.
- Dựng đường thẳng PM.
- Từ N dựng đường thẳng song song với PM cắt tia Oy tại Q.
Đoạn thẳng PQ = a cần dựng..
* Chứng minh:
Theo cách dựng, ta có: PM // NQ.
Trong ΔONQ ta có: PM // NQ