Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gợi ý :
a) y = 2 => x = 2 hoặc -2 ( do có thể < 0 hay > 0 )
b) S(OAB) = 1 => |x| = 1 => x = 1 hoặc -1
c) Gọi khoảng cách từ O tới (d) là OH
OH bé hơn hoặc bằng khoảng cách 2 của O tới điểm cố định trên Oy
=> max = 2 khi d song^2 Ox => x = 0 => đúng mọi m
d) Thay vào biểu thức hệ thức lượng => khoảng cách từ O tới điểm mà d cắt trên Ox là 0 => d trùng Oy
e) thay x vào có kết quả
f) cắt tại điểm > 2 => biểu thức biểu diễn x > 2 ( -2/(m+3) )

PT giao Ox, Oy là:
\(y=0\Leftrightarrow x=\dfrac{2}{2m+1}\Leftrightarrow A\left(\dfrac{2}{2m+1};0\right)\Leftrightarrow OA=\dfrac{2}{\left|2m+1\right|}\\ x=0\Leftrightarrow y=-2\Leftrightarrow B\left(0;-2\right)\Leftrightarrow OB=2\)
\(a,\) Gọi H là chân đường cao từ O đến (d) \(\Leftrightarrow OH=\sqrt{2}\)
Ap dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{\left(2m+1\right)^2}{4}+\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{\left(2m+1\right)^2}{4}=\dfrac{1}{4}\Leftrightarrow4m^2+4m+1=1\\ \Leftrightarrow4m\left(m+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=-1\end{matrix}\right.\)
\(b,S_{AOB}=\dfrac{1}{2}OA\cdot OB=\dfrac{1}{2}\Leftrightarrow OB\cdot OA=1\\ \Leftrightarrow\dfrac{2}{\left|2m+1\right|}\cdot2=1\Leftrightarrow\left|2m+1\right|=4\\ \Leftrightarrow\left[{}\begin{matrix}2m+1=4\\2m+1=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{2}\\m=-\dfrac{5}{2}\end{matrix}\right.\)

Cho \(x=0\Rightarrow y=-3\)
Cho \(y=0\Rightarrow x=3\)
\(A\left(3;0\right)\in\left(d\right);B\left(0;-3\right)\in\left(d\right)\)
Ta có: Tam giác OAB vuông tại O
\(OA=\left|3\right|=3\left(đvđd\right)\)
\(OB=\left|-3\right|=3\left(đvđd\right)\)
\(AB^2=OA^2+OB^2\)
\(\Leftrightarrow AB=\sqrt{3^2+3^2}=3\sqrt{2}\left(đvđd\right)\)
Kẻ \(OH\perp AB\) (\(H\in AB\) )
\(S_{OAB}=\dfrac{OA.OB}{2}=\dfrac{3.3}{2}=\dfrac{9}{2}\left(đvdt\right)\)
\(\Leftrightarrow\dfrac{9}{2}=\dfrac{1}{2}.AB.OH\)
\(\Leftrightarrow\dfrac{9}{4}=2\sqrt{3}.OH\)
\(\Leftrightarrow OH=\dfrac{3\sqrt{3}}{8}\left(đvđd\right)\)

d ∩ O y = B x B = 0 ⇒ y B = 4 ⇔ B 0 ; 4 ⇒ O B = 4 = 4 d ∩ O x = A y A = 0 ⇔ m 2 – 2 m + 2 x A + 4 = 0 x A = x A = − 4 m 2 − 2 m + 2 ⇒ A − 4 m 2 − 2 m + 2 ; 0 ⇒ O A − 4 m 2 − 2 m + 2
\ S Δ A O B = 1 2 O A . O B = 1 2 .4. − 4 m 2 − 2 m + 2 = 8 m − 1 2 + 1
Ta có m – 1 2 + 1 ≥ 1 ∀ m
Do đó S Δ A O B = 8 m − 1 2 + 1 ≤ 8 1 = 8
Dấu “=” xảy ra khi m – 1 = 0 ⇔ m = 1
Hay tam giác OAB có diện tích lớn nhất là 8 khi m = 1
Đáp án cần chọn là: A

a:Thay x=-2 và y=0 vào (d), ta được:
-2(m-1)+4=0
=>-2(m-1)=-4
=>m-1=2
=>m=3
b: (d): y=2x+4
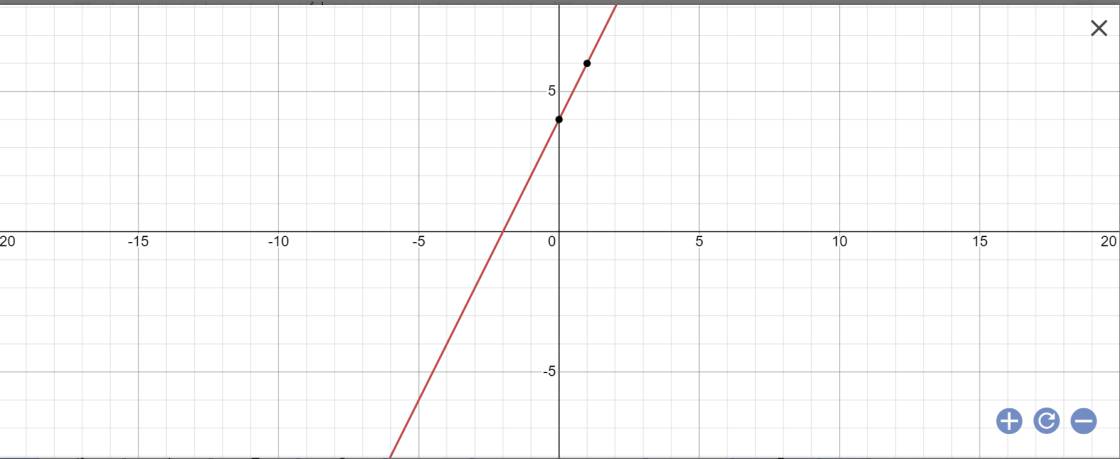
Khoảng cách từ O đến (d) là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\left(m^2+1\right)+0\cdot\left(-1\right)+2\right|}{\sqrt{\left(m^2+1\right)^2+1}}=\dfrac{2}{\sqrt{\left(m^2+1\right)^2+1}}\)
\(\sqrt{\left(m^2+1\right)^2+1}>=\sqrt{1+1}=\sqrt{2}\)
=>\(d\left(O;\left(d\right)\right)=\dfrac{2}{\sqrt{\left(m^2+1\right)^2+1}}< =\sqrt{2}\forall m\)
Dấu '=' xảy ra khi m=0