Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của Mafia - Toán lớp 9 - Học toán với OnlineMath
Em có thể tham khảo tại đây nhé.

OMABICDEF
a) Ta thấy OAM và OBM là các tam giác vuông có chung cạnh huyền OM nên A, O, B, M cùng thuộc đường tròn đường kính OM.
b) Theo tính chất hai tiếp tuyến cắt nhau thì MA = MB và MI là tia phân giác góc AMB.
Vậy thì tam giác MAB cân tại M, có phân giác MI đồng thời là đường cao.
Vậy nên \(OM\perp AB\) tại I.
c) Do D thuộc đường tròn (O) nên OC = OB = OD.
Suy ra tam giác BDC vuông tại D.
Xét tam giác vuông CBM, đường cao BD, ta có: \(MD.MC=BM^2\) (Hệ thức lượng)
Xét tam giác vuông OBM, đường cao BI, ta có: \(MI.MO=BM^2\) (Hệ thức lượng)
Vậy nên MD.MC = MI.MO
d) Ta thấy CEF và CAF là các tam giác vuông có chung cạnh huyền CF nên FAEC nội tiếp đường tròn đường kính CF.
\(\Rightarrow\widehat{FCE}=\widehat{EAB}\) (Hai góc nội tiếp cùng chắn cung CO)
Lại có O,E, A, M, B cùng thuộc đường tròn đường kính OM nên \(\widehat{EAB}=\widehat{EMB}\) (Hai góc nội tiếp cùng chắn cung EB)
\(\Rightarrow\widehat{FCE}=\widehat{EMB}\)
Ta có \(\widehat{EMB}+\widehat{ECB}=90^o\Rightarrow\widehat{FCE}+\widehat{ECB}=90^o\)
\(\Rightarrow\widehat{FCB}=90^o\)
Vậy FC là tiếp tuyến của đường tròn (O).

\(1,a)\hept{\begin{cases}10x-9y=1\\15x+21y=36\end{cases}}\)
\(< =>\hept{\begin{cases}5x+30y=35\\10x+9y=1\end{cases}}\)
\(< =>\hept{\begin{cases}10x+60y=70\\10x+9y=1\end{cases}}\)
\(< =>51y=69< =>y=\frac{69}{51}=\frac{23}{17}\)
Thay \(y=\frac{23}{17}\)vào \(10x-9y=1\)có :
\(10x-9y=1\)\(< =>10x=1+\frac{207}{17}=\frac{224}{17}\)
\(< =>x=\frac{224}{170}=\frac{112}{85}\)
Vậy nghiệm của hệ pt trên là \(\left\{\frac{112}{85};\frac{23}{17}\right\}\)
P/s : Số khá xấu nên ko chắc :P
\(b)\hept{\begin{cases}4x+y=2\\8x+3y=5\end{cases}}\)
\(< =>\hept{\begin{cases}8x+2y=4\\8x+3y=5\end{cases}}\)
\(< =>y=1\)
Thay \(y=1\)vào \(4x+y=2\)có :
\(4x+y=2\)
\(< =>4x=2-1=1< =>x=\frac{1}{4}\)
Vậy nghiệm của hệ pt trên là \(\left\{\frac{1}{4};1\right\}\)
\(c)\hept{\begin{cases}x-y=m\\2x+y=4\end{cases}}\)
\(< =>3x=4+m\)
\(< =>x=\frac{4+m}{3}\)
Thay \(x=\frac{4+m}{3}\)vào \(x-y=m\)có :
\(x-y=m\)\(< =>\frac{4+m}{3}-\frac{3y}{3}=\frac{3m}{3}\)
\(< =>4+m-3y=3m\)
\(< =>4-3y=2m\)
\(< =>4-2m=3y\)
\(< =>y=\frac{2\left(2-m\right)}{3}\)
Vậy nghiệm của hệ pt trên là \(\left\{\frac{4+m}{3};\frac{2\left(2-m\right)}{3}\right\}\)
\(d)\hept{\begin{cases}3x+2y=6\\x-y=2\end{cases}}\)
\(< =>\hept{\begin{cases}3x+2y=6\\x=2+y\end{cases}}\)
\(< =>3\left(2+y\right)+2y=6\)
\(< =>6+3y+2y=6\)
\(< =>5y=0< =>y=0\)
Thay \(y=0\)vào \(x-y=2\)có :
\(x-y=2< =>x=2\)
Vậy nghiệm của hệ pt trên là \(\left\{2;0\right\}\)
\(e)\hept{\begin{cases}2x-3y=1\\-4x+6y=2\end{cases}}\)
\(< =>\hept{\begin{cases}x=\frac{1+3y}{2}\\-4x+6y=2\end{cases}}\)
\(< =>-4\left(\frac{1+3y}{2}\right)+6y=2\)
\(< =>-\frac{4+12y}{2}+\frac{12y}{2}=\frac{4}{2}\)
\(< =>-\left(4+12y\right)+12y=4\)
\(< =>-4-12y-4=-12y\)
\(< =>-8-12y=-12y\)
\(< =>12y=12y+8\)(vô lí)
Nên hệ pt trên vô nghiệm :))
\(f)\hept{\begin{cases}2x+3y=5\\5x-4y=1\end{cases}}\)
\(< =>\hept{\begin{cases}x=\frac{5-3y}{2}\\5x-4y=1\end{cases}}\)
\(< =>5\left(\frac{5-3y}{2}\right)-4y=1\)
\(< =>\frac{25-15y}{2}-\frac{8y}{2}=\frac{2}{2}\)
\(< =>25-15y-8y=2\)
\(< =>25-23y=2\)
\(< =>23y=25-2=23\)
\(< =>y=1\)
Thay \(y=1\)vào \(2x+3y=5\)có :
\(2x+3y=5< =>2x+3=5\)
\(< =>2x=5-3=2< =>x=1\)
Vậy nghiệm của hệ pt trên là \(\left\{1;1\right\}\)
Câu 1 :
a) \(\hept{\begin{cases}10x-9y=1\\15x+21y=36\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}10x-9y=1\\10x+14y=24\end{cases}}\)
\(\Leftrightarrow23y=23\)
\(\Leftrightarrow y=1\)
Thay \(y=1\)vào \(10x-9y=1\)ta được:
\(10x-9=1\Leftrightarrow x=1\)
Vậy \(\left(x;y\right)=\left(1;1\right)\)
p/s: mấy câu còn lại chắc ๖ۣۜNhi's Godッ làm ok rồi

Ta có:
\(\sqrt{2016a+\frac{\left(b-c\right)^2}{2}}=\sqrt{2016a+\frac{b^2-2bc+c^2}{2}}=\sqrt{2016a+\frac{b^2+2bc+c^2-4bc}{2}}\)
\(=\sqrt{2016a+\frac{\left(b+c\right)^2-4bc}{2}}=\sqrt{2016a+\frac{\left(b+c\right)^2}{2}-2bc}\)
\(\le\sqrt{2016a+\frac{\left(b+c\right)^2}{2}}\left(b,c\ge0\right)=\sqrt{2016a+\frac{\left(a+b+c-a\right)^2}{2}}\)
\(=\sqrt{2016a+\frac{\left(1008-a\right)^2}{2}}=\sqrt{\frac{\left(1008+a\right)^2}{2}}=\frac{1008+a}{\sqrt{2}}\left(a\ge0\right)\)
Tương tự cho 2 BĐT còn lại ta cũng có:
\(\sqrt{2016b+\frac{\left(c-a\right)^2}{2}}\le\frac{1008+b}{\sqrt{2}};\sqrt{2016c+\frac{\left(a-b\right)^2}{2}}\le\frac{1008+c}{\sqrt{2}}\)
Cộng theo vế 3 BĐT trên ta có:
\(VT\le\frac{3\cdot1008+\left(a+b+c\right)}{\sqrt{2}}=\frac{4\cdot1008}{\sqrt{2}}=2016\sqrt{2}\)

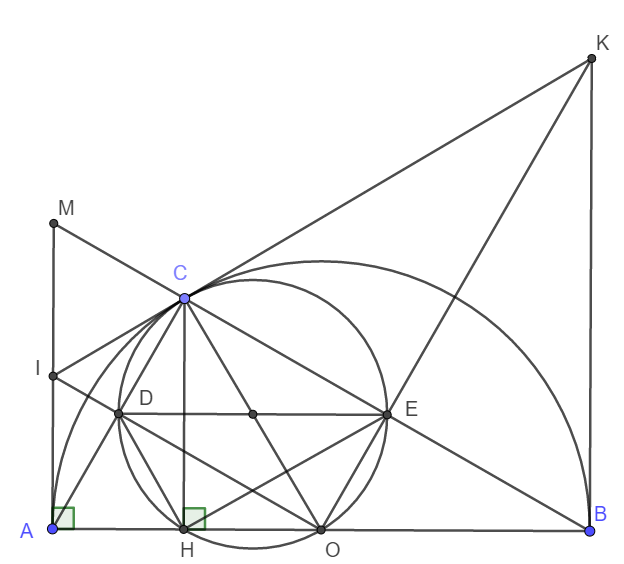
a) Do C thuộc nửa đường tròn nên \(\widehat{ACB}=90^o\) hay AC vuông góc MB.
Xét tam giác vuông AMB có đường cao AC nên áp dụng hệ thức lượng ta có:
\(BC.BM=AB^2=4R^2\)
b) Xét tam giác MAC vuông tại C có CI là trung tuyến ứng với cạnh huyền nên IM = IC = IA
Vậy thì \(\Delta ICO=\Delta IAO\left(c-c-c\right)\)
\(\Rightarrow\widehat{ICO}=\widehat{IAO}=90^o\)
Hay IC là tiếp tuyến tại C của nửa đường tròn.
c) Xét tam giác vuông AMB có đường cao AC, áp dụng hệ thức lượng ta có:
\(MB.MC=MA^2=4IC^2\Rightarrow IC^2=\frac{1}{4}MB.MC\)
Xét tam giác AMB có I là trung điểm AM, O là trung điểm AB nên IO là đường trung bình tam giác ABM.
Vậy thì \(MB=2OI\Rightarrow MB^2=4OI^2\) (1)
Xét tam giác vuông MAB, theo Pi-ta-go ta có:
\(MB^2=MA^2+AB^2=MA^2+4R^2\) (2)
Từ (1) và (2) suy ra \(4OI^2=MA^2+4R^2.\)
d) Do IA, IC là các tiếp tuyến cắt nhau nên ta có ngay \(AC\perp IO\Rightarrow\widehat{CDO}=90^o\)
Tương tự \(\widehat{CEO}=90^o\)
Xét tứ giác CDOE có \(\widehat{CEO}=\widehat{CDO}=90^o\)mà đỉnh E và D đối nhau nên tứ giác CDOE nội tiếp đường tròn đường kính CO.
Xét tứ giác CDHO có: \(\widehat{CHO}=\widehat{CDO}=90^o\) mà đỉnh H và D kề nhau nên CDHO nội tiếp đường tròn đường kính CO.
Vậy nên C, D, H , O, E cùng thuộc đường tròn đường kính CO.
Nói cách khác, O luôn thuộc đường tròn ngoại tiếp tam giác HDE.
Vậy đường tròn ngoại tiếp tam giác HDE luôn đi qua điểm O cố định.