K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
GN
3
DD
3 tháng 8 2015
-67:x dư 7, -105:x dư 5
=> -67-7 chia hết cho x, -105-5 chia hết cho x
-74 chia hết x, -110 chia hết x. => xEU(-74,-110) và x>0
-74=-(2.37)
-110=-(2.5.11)
UCLN(-74,-110)=2
=> Ư(-74,-110)=Ư(2)=1,-1,2,-2. => x E{1,-1,2,-2). Vì x>0 nên x=1, x=2
M
14 tháng 12 2017
67:x dư 7=>67-7 chia hết cho x=>60 chia hết cho x
93:x dư 9=>93-9 chia hết cho x=>84 chia hết cho x
60 chia hết cho x
84 chia hết cho x
=>x thuộc ƯCLN(60;84)
60=2^2.3.5
84=2^2.3.7
ƯCLN(60;84)=2^2.3=12
Vì x thuộc ƯCLN(60;84)=>x=12
21 tháng 12 2016
ta có
67:x( du 7)
93:x (du 9)
=>67-7 chia hết cho x
93-9 chia hết cho x
=>60 chia hết cho x
84 chia hết cho x
=>x thuộc ÚC (60,84)
lại có
60=2^2.3.5
84=2^2.3.7
=>UCLN(60,84)=2^2.3=12
=>UC(60,84)=U(12)={1,2,3,4,6,12}
vay xthuoc {1,2,3,4,6,12}
19 tháng 8 2015
5 số tự nhiên đó có dạng: a + a+1+a+2+a+3+a+4 = a x 5 + 10 = 5 x (a+2)
Vậy tổng số số tự nhiên liên tiếp luôn luôn chia hết cho 5
KT
4 tháng 2 2018
a) \(\left(-67\right).\left(2-301\right)-301.67\)
\(=-67.2+67.301-301.67\)
\(=-67.2=134\)
b) \(35.99+19\left(-7\right).5\)
\(=35.99-35.19\)
\(=35.\left(99-19\right)\)
\(=35.80=2800\)
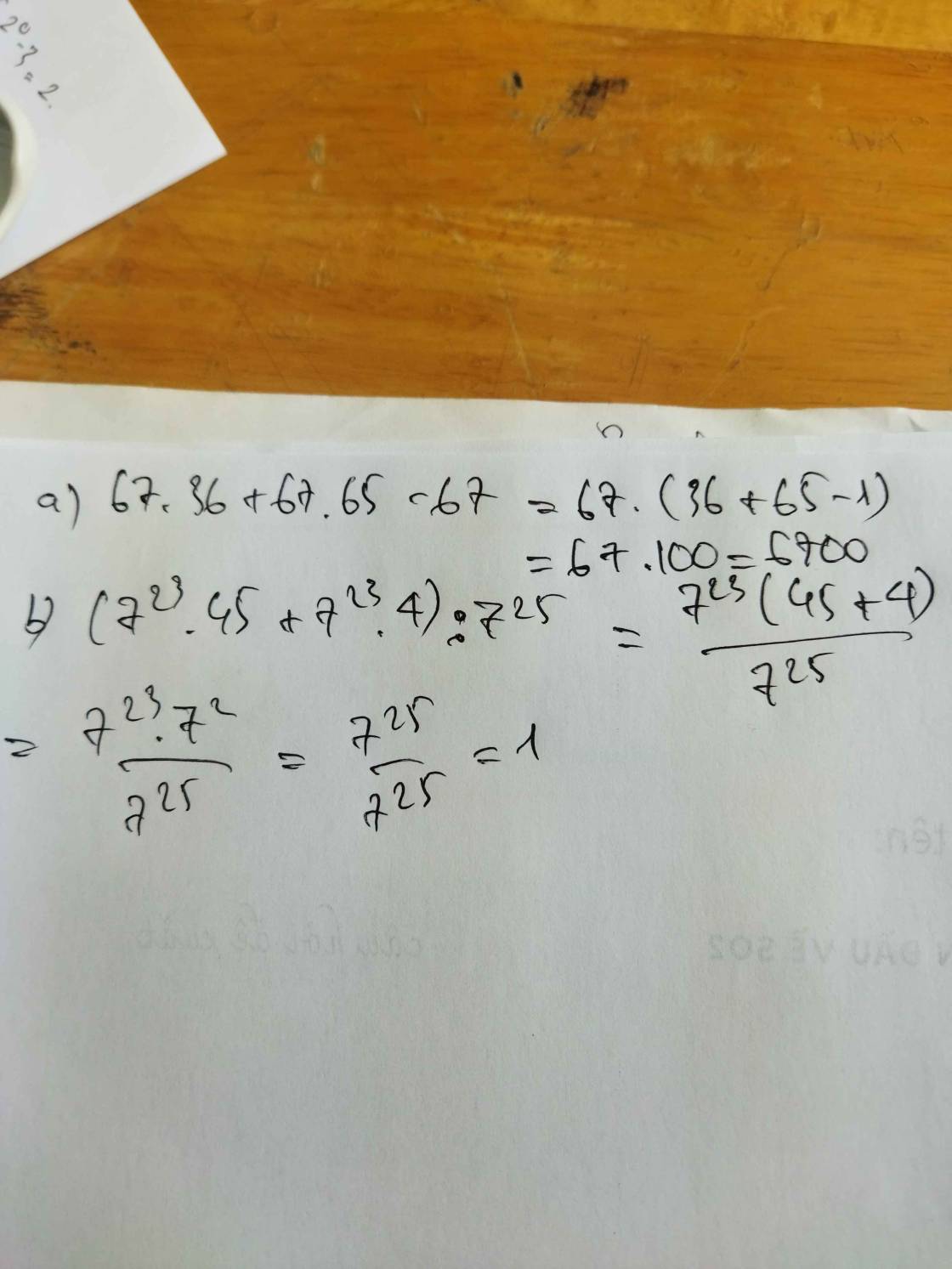
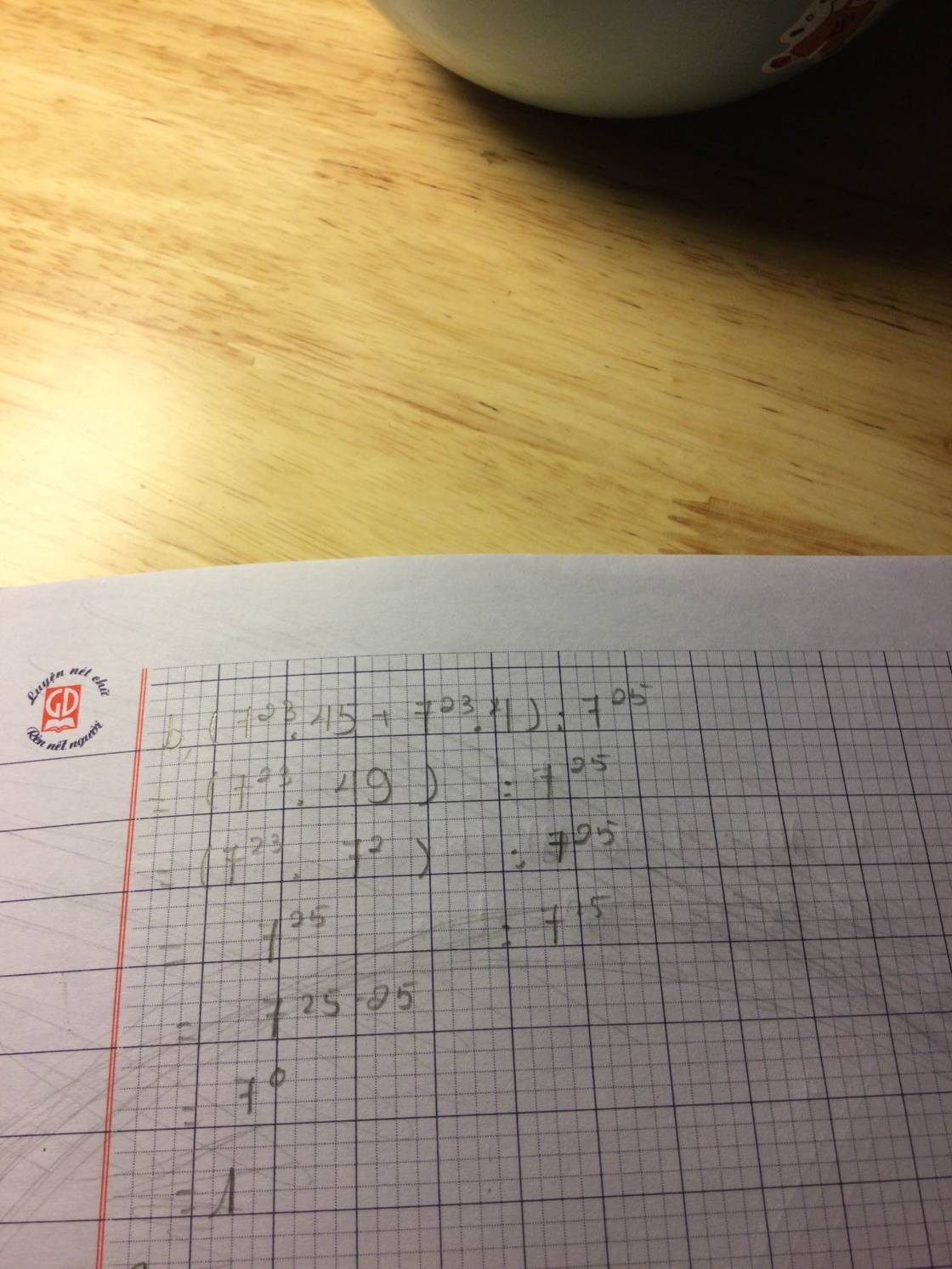
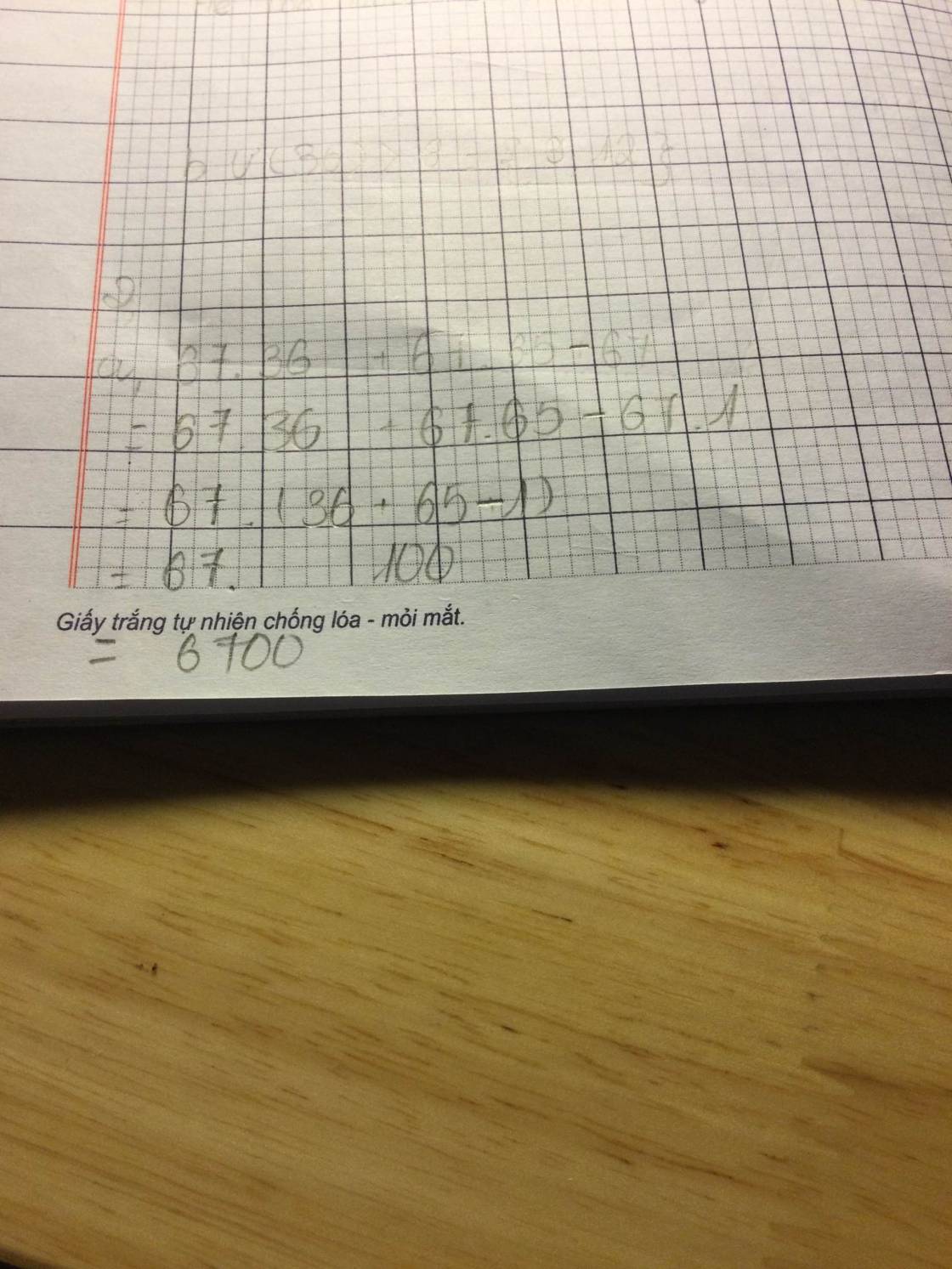
=> (67-7) chia hết cho (x+1)
=> 60 chia hết (x+1)
Để 60 chia hết (x+1) thì (x+1) là số nguyên
=> (x+1)€{\(\pm\)1;\(\pm\)2;...(bạn viết hết các ước của 60)}
Vì 67 chia (x+1) dư 7 nên (x+1) lớn 7
=> (x+1)€{10;12;15;20;30;60}
=> x€{9;11;14;19;29;59}
Vậy...