K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
10 tháng 10 2023
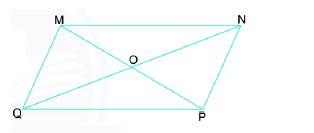
Hình bình hành MNPQ có:
- Các góc đối bằng nhau nên góc đỉnh M của hình bình hành MNPQ bằng góc đỉnh P
- Điểm O là trung điểm của MP nên OM=OP (tính chất hai đường chéo cắt nhau tại trung điểm của mỗi đường).
Điểm O là trung điểm của NQ nên ON=OQ (tính chất hai đường chéo cắt nhau tại trung điểm của mỗi đường).
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
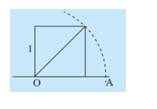
Đường chéo của hình vuông có độ dài đường chéo là 1 bằng \(\sqrt 2 \).
\(\sqrt 2 \) là số vô tỉ.
MD
19 tháng 9 2023
Lời giải:
Ta quan sát thấy hình vuông trong hình có độ dài cạnh là 1 nên độ dài đường chéo của nó là √22. Mặt khác, ta thấy độ dài đường chéo của hình vuông bằng độ dài cạnh OA. Do đó độ dài cạnh OA = √22.
Mà √22 không phải số hữ tỉ nên OA không phải số hữu tỉ.
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
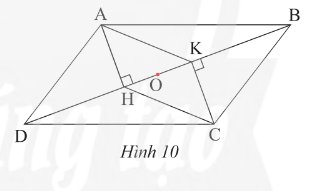
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\) (1)
Vì \(AKCH\) là hình bình hành (gt)
Mà \(O\) là trung điểm của \(AC\)
Suy ra \(O\) là trung điểm của \(HK\)
15 tháng 10 2021
Nửa chu vi hình chữ nhật ABCD là:
\(120\div2=60\left(cm\right)\)
Chiều dài hình chữ nhật là:
\(\left(60+10\right)\div2=35\left(cm\right)\)
Chiều rộng hình chữ nhật là:
\(35-10=25\left(cm\right)\)
Diện tích hình bình hành ABEG cũng chính là diện tích hình chữ nhật ABCD
( Vì chiều cao và cạnh tương ứng của hình bình hành cũng chính bằng chiều rộng và chiều dài hình chữ nhật )
Vậy diện tích hình bình hành ABEG là:
\(35.25=875\left(cm^2\right)\)
PT
2
CM
21 tháng 3 2018
Đáp án là C
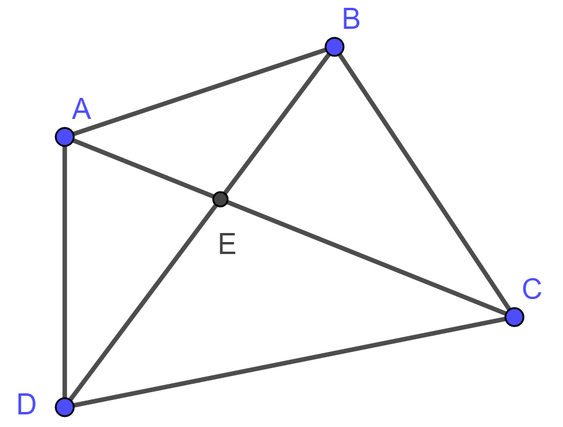
Trên hình vẽ trên có các tam giác là:
ΔABE; ΔADE; ΔABD; ΔBCE; ΔDCE; ΔBCD; ΔABC; ΔACD
Vậy có tất cả 8 tam giác trên hình vẽ
HQ
Hà Quang Minh
Giáo viên
3 tháng 10 2023
1) Ta đo được: AB = CD; BC = AD. Vậy các cạnh đối của hình bình hành bằng nhau
2) OA = OC; OB = OD
3) + Khi đặt eke vuông góc với AB, ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
+ Khi đặt eke vuông góc với BC, ta thấy eke cũng vuông góc với AD. Do đó BC và AD song song với nhau.
Vậy các cạnh đối của hình bình hành song song với nhau.
4) Gấp giấy, ta thấy các góc đối của hình bình hành bằng nhau.
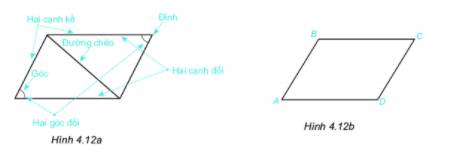
Có bao nhiêu hình bình hành
Có hai hình bình hành.