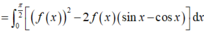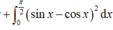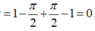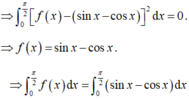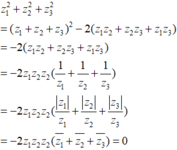cho (0;r) và dây ef khác đường kính từ o kẻ ok vuông ef (k thuộc ef) b, Biết R=6 OK=2.Tính
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
25 tháng 10 2023
\(\dfrac{2x-1}{2x+1}\\ a,đkxđ:2x+1\ne0\Leftrightarrow2x\ne-1\Leftrightarrow x\ne-\dfrac{1}{2}\\ B,\)
Khi `x=0` thì Ta có :
\(\dfrac{2x-1}{2x+1}=\dfrac{2\cdot0-1}{2\cdot0+1}=\dfrac{0-1}{0+1}=-\dfrac{1}{1}=-1\)
H9
HT.Phong (9A5)
CTVHS
25 tháng 10 2023
A. Điều kiện xác định là:
\(2x+1\ne0\)
\(\Leftrightarrow2x\ne-1\)
\(\Leftrightarrow x\ne-\dfrac{1}{2}\)
B. Thay x = 0 biểu thức ta có:
\(\dfrac{2\cdot0-1}{2\cdot0+1}=\dfrac{-1}{1}=-1\)
T
6
TM
12 tháng 7 2017
\(x^2+\frac{1}{x^2}=7\Leftrightarrow\left(x+\frac{1}{x}\right)^2-2=7\Leftrightarrow\left(x+\frac{1}{x}\right)^2=9\Leftrightarrow x+\frac{1}{x}=3\)(vì x>0)
<=>\(\left(x+\frac{1}{x}\right)^3=27\Leftrightarrow x^3+3\left(x+\frac{1}{x}\right)+\frac{1}{x^3}=27\Leftrightarrow x^3+\frac{1}{x^3}+3.3=27\Leftrightarrow x^3+\frac{1}{x^3}=18\)
Xét \(\left(x+\frac{1}{x}\right)\left(x^4+\frac{1}{x^4}\right)=x^5+x^3+\frac{1}{x^3}+\frac{1}{x^5}=x^5+\frac{1}{x^5}+18\)
Mặt khác:
\(\left(x+\frac{1}{x}\right)\left(x^4+\frac{1}{x^4}\right)=\left(x+\frac{1}{x}\right)\left[\left(x^2+\frac{1}{x^2}\right)^2-2\right]=\left(x+\frac{1}{x}\right)\left(7^2-2\right)=3.47=141\)
=>\(x^5+\frac{1}{x^5}+18=141\Leftrightarrow x^5+\frac{1}{x^5}=123\)
CM
20 tháng 11 2017
Đáp án B
z 1 2 + z 2 2 + z 3 2 = z 1 + z 2 + z 3 2 - 2 ( z 1 z 2 + z 2 z 3 + z 3 z 1 = - 2 z 1 z 2 z 2 1 z 1 + 1 z 2 + 1 z 3 = - 2 z 1 z 2 z 2 z 1 z 1 + z 2 z 2 + z 3 z 3 = - 2 z 1 z 2 z 2 z 1 + z 2 + z 3 = 0
CM
20 tháng 4 2018
Đáp án B.
Ta có ∫ 0 π 4 f ' x sin 2 x d x
Đặt u = sin 2 x d v = f ' x ⇒ d u = 2 cos 2 xdx v = f x suy ra
∫ 0 π 4 f ' x sin 2 x d x = sin 2 x f x π 4 0 − ∫ 0 π 4 2 cos 2 x . f x d x
⇒ − 2 ∫ 0 π 4 c o s 2 x . f x d x = − π 4 ⇒ ∫ 0 π 4 c o s 2 x . f x d x = π 8
Lại có: ∫ 0 π 4 c o s 2 2 x . f x d x = π 8 ⇒ ∫ 0 π 4 f x − c o s 2 x 2 d x = 0 ⇒ f x = c o s 2 x
Do đó ∫ 0 π 8 f 2 x d x = ∫ 0 π 8 c o s 4 x d x = sin 4 x 4 π 8 0 = 1 4 .