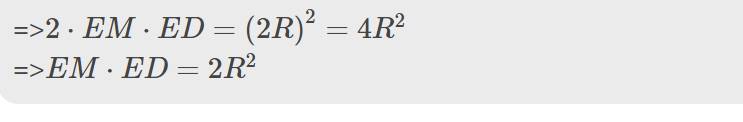Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
- Vì ON = OP < R/2, nên N và P nằm trong đường tròn tâm O, nên A, C, B, D đều nằm trên đường tròn (O).
- Vì AC // BD, nên theo định lí của dây cung, ta có: AM = MC và BM = MD.
- Ta có: ∠BAC = ∠BMC (do ABMC là hình bình hành) và ∠ACB = ∠AMB (do ABMC là hình bình hành).
- Vậy tứ giác ABMC là tứ giác cùng tứ giác nội tiếp, nên ta có: ∠BMC + ∠AMB = 180°.
- Từ đó, ta có: ∠BAC + ∠ACB = 180°.
- Vậy tứ giác ABCD là tứ giác điều hòa.
- Gọi K' là giao điểm của BD và AO. Ta cần chứng minh K', Q, A đồng quy.
- Ta có: ∠QAC = ∠QDC (do AC // BD) và ∠QCA = ∠QCB (do ABMC là hình bình hành).
- Vậy tứ giác AQCD là tứ giác cùng tứ giác nội tiếp, nên ta có: ∠QDC + ∠QCA = 180°.
- Từ đó, ta có: ∠QAC + ∠QCA = 180°.
- Vậy tứ giác AQCK' là tứ giác điều hòa.
- Vậy K', Q, A đồng quy. - Vậy KQ, BD, AO đồng quy.\
Xin tick!!

\(a,\widehat{DHF}=90^0\)(góc nt chắn nửa đg tròn) nên \(DH\perp EF\)
\(b,\left\{{}\begin{matrix}OK\perp HF\\DH\perp HF\end{matrix}\right.\Rightarrow OK//DH;FO=OD\Rightarrow FK=HK\\ \left\{{}\begin{matrix}FO=OD\\FK=HK\end{matrix}\right.\Rightarrow OK.là.đtb.\Delta DFH\)
Lại có \(FD=2FO=10\left(cm\right);DH=\sqrt{FD^2-FH^2}=6\left(cm\right)\left(pytago\right)\)
\(\Rightarrow OK=\dfrac{1}{2}DH=3\left(cm\right)\)
\(c,\) Áp dụng HTL tam giác
\(\Rightarrow DH^2=HE\cdot HF\)
Mà \(2OK=DH\Rightarrow\left(2OK\right)^2=HE\cdot HF\Rightarrow4OK^2=HE\cdot HF\)

a: Xét ΔOEA vuông tại E có EM là đường cao
nên \(OM\cdot OA=OE^2\)
=>\(OA=\dfrac{10^2}{6}=\dfrac{50}{3}\left(cm\right)\)
ΔOEA vuông tại E
=>\(OE^2+EA^2=OA^2\)
=>\(EA^2+10^2=\left(\dfrac{50}{3}\right)^2\)
=>\(EA^2=\left(\dfrac{40}{3}\right)^2\)
=>EA=40/3(cm)
Xét ΔEAO vuông tại E có EM là đường cao
nên \(EM\cdot OA=EA\cdot EO\)
=>\(EM\cdot\dfrac{50}{3}=10\cdot\dfrac{40}{3}\)
=>\(EM\cdot50=10\cdot40\)
=>EM=400/50=8(cm)
Ta có: ΔOEF cân tại O
mà OM là đường cao
nên M là trung điểm của EF và OM là phân giác của góc EOF
=>\(EF=2\cdot EM=16\left(cm\right)\)
b: Xét ΔOEA và ΔOFA có
OE=OF
\(\widehat{EOA}=\widehat{FOA}\)
OA chung
Do đó: ΔOEA=ΔOFA
=>\(\widehat{OEA}=\widehat{OFA}=90^0\)
=>AFlà tiếp tuyến của (O)
c: Xét (O) có
ΔEFC nội tiếp
EC là đường kính
Do đó: ΔEFC vuông tại F
=>EF\(\perp\)FC tại F
=>CF\(\perp\)ED tại F
Xét ΔECD vuông tại C có EF là đường cao
nên \(EF\cdot ED=EC^2\)
=>\(2\cdot EM\cdot ED=\left(2R\right)^2=4R^2\)
=>\(EM\cdot ED=2R^2\)

a: góc MHO+góc MKO=180 độ
=>MHOK nội tiêp
C,N,D,F cùng thuộc (O)
nên CNDF nội tiếp
b: Xét ΔCKM vuông tại K và ΔCHO vuông tại H có
góc KCM chung
=>ΔCKM đồng dạng voi ΔCHO
=>CK/CH=CM/CO
=>CK*CO=CH*CM

bạn ơi cho mình hỏi bước thứ nhất bạn làm theo định lí gì v bạn

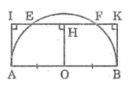
Ta có: AI ⊥ EF (gt)
BK ⊥ EF (gt)
Suy ra: AI // BK
Suy ra tứ giác ABKI là hình thang
Kẻ OH ⊥ EF
Suy ra: OH // AI // BK
Ta có: OA = OB (= R)
Suy ra: HI = HK
Hay: HE + EI = HF + FK (1)
Lại có: HE = HF (đường kính dây cung) (2)
Từ (1) và (2) suy ra: IE = KF