Cho tam giác $ABC$ có hai đường cao $BB'$ và $CC'$. Gọi $O$ là trung điểm của $BC$. So sánh độ dài hai đoạn thẳng $BC$ và $B'C'$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


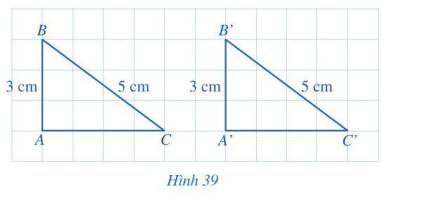
Xét hai tam giác vuông: ∆ABC và ∆A'B'C' có:
BC = B'C' = 5 cm
AB = A'B' = 3 cm
⇒ ∆ABC = ∆A'B'C' (cạnh huyền - cạnh góc vuông)
⇒ AC = A'C' (hai cạnh tương ứng)

Lời giải :
Ta có : \(\frac{AB'}{AB}=\frac{AC'}{AC}\)( GT ) ( 1 )
+) Đường thẳng a đi qua B' song song với BC ( GT )
\(B'C''//BC\)( vì đường thẳng a cắt AC tại C'' )
\(\Rightarrow\frac{AB'}{AB}=\frac{AC''}{AC}\)( Định lí Ta lét ) ( 2 )
Từ ( 1 ) và ( 2 )
\(\Rightarrow AC'=AC''\)

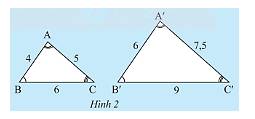
a) Từ kí hiệu của hình vẽ ta thấy các cặp góc bằng nhau là:
\(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\)
b) Ta có:
\(\frac{{A'B'}}{{AB}} = \frac{6}{4} = \frac{3}{2};\frac{{A'C'}}{{AC}} = \frac{{7,5}}{5} = \frac{3}{2};\frac{{B'C'}}{{BC}} = \frac{9}{6} = \frac{3}{2}\).
Ta thấy, \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{3}{2}\)
a: góc A=góc A'; góc B=góc B'; góc C=góc C'
b: A'B'/AB=A'C'/AC=B'C'/BC

a: Ta có: ΔBEH vuông tại H
nên \(\widehat{BEH}< 90^0\)
=>\(\widehat{BEA}>90^0\)
=>BA>BE
b: Ta có: ΔEHC vuông tại H
nên \(\widehat{HEC}< 90^0\)
=>\(\widehat{AEC}>90^0\)
hay CA>CE
c: Xét ΔEBC có HB<HC
mà HB là hình chiếu của EB trên BC
và HC là hình chiếu của EC trên BC
nên EB<EC

a: Xét ΔABC có AC>AB
mà góc đối diện với cạnh AC là góc ABC
và góc đối diện với cạnh AB là góc ACB
nên \(\widehat{ABC}>\widehat{ACB}\)
b: Xét ΔABC có AC>AB
mà hình chiếu của AC trên BC là HC
và hình chiếu của AB trên BC là HB
nên HC>HB
Xét tứ giác BC'B'C có \(\widehat{BC'C}=\widehat{BB'C}=90^0\)
nên BC'B'C là tứ giác nội tiếp đường tròn đường kính BC
=>BC'B'C là tứ giác nội tiếp đường tròn tâm O, đường kính BC
Xét (O) có
BC là đường kính
B'C' là dây
Do đó: B'C'<BC