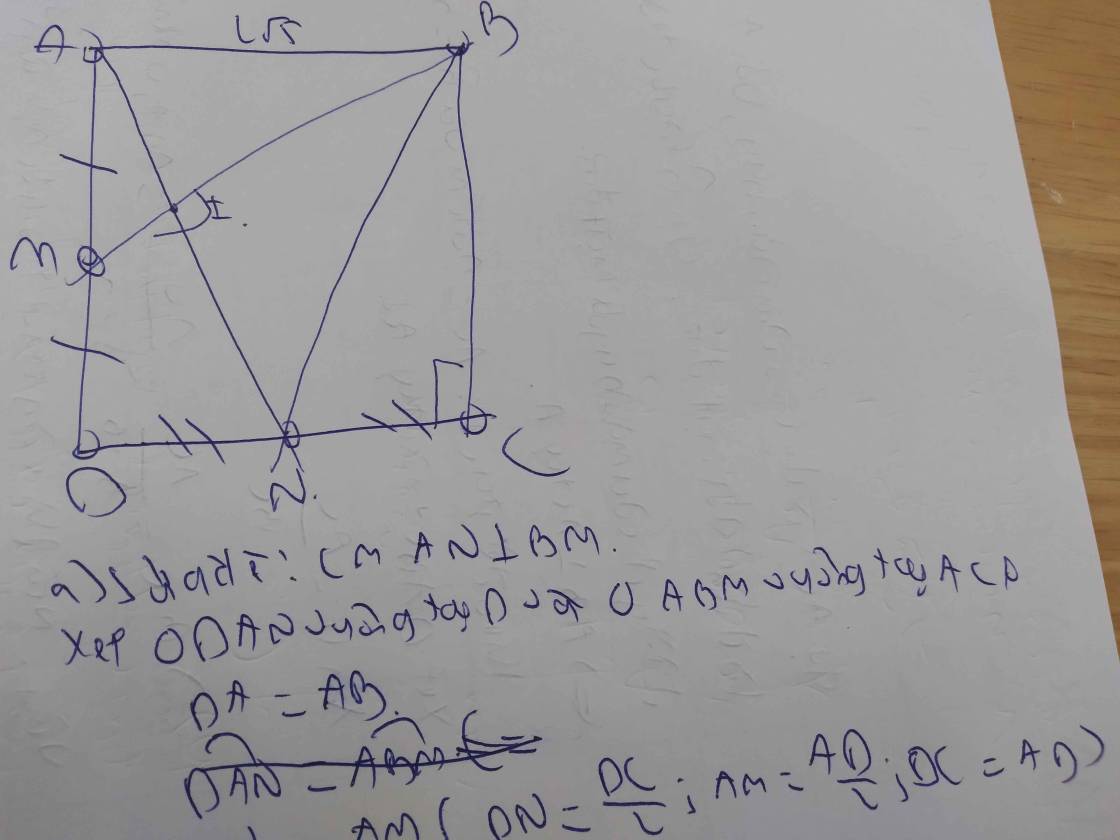
Cho hình vuông ABCD có cạnh bằng 2 căn 5cm. Gọi M,N lần lượt là trung điểm của AD,DC
và I là giao điểm của AN,BM và.
1. Chứng minh rằng AN vuông góc với MB
2. Tính AI,MI.
3. Tính diện tích tứ giác BINC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
DO ABCD là hình vuông \(\Rightarrow\widehat{ACD}=45^0\)
\(\Rightarrow\widehat{ACD}=\widehat{EBN}\)
Mà \(\widehat{ACD}\) và \(\widehat{EBN}\) cùng chắn EN
\(\Rightarrow\) Tứ giác BENC nội tiếp
\(\Rightarrow\widehat{BEN}+\widehat{BCN}=180^0\)
\(\Rightarrow\widehat{BEN}=180^0-\widehat{BCN}=180^0-90^0=90^0\)
\(\Rightarrow NE\perp BM\) tại E
b.
Tương tự ta có tứ giác ABFM nội tiếp (\(\widehat{MAF}=\widehat{MBF}=45^0\) cùng chắn MF)
\(\Rightarrow\widehat{BFM}+\widehat{BAM}=180^0\)
\(\Rightarrow\widehat{BFM}=90^0\Rightarrow MF\perp BN\)
\(\Rightarrow I\) là trực tâm của tam giác BMN
\(\Rightarrow BI\perp MN\)
c.
Gọi H là giao điểm BI và MN
Do E và F cùng nhìn MN dưới 1 góc vuông
\(\Rightarrow\) Tứ giác EFMN nội tiếp
\(\Rightarrow\widehat{EMN}+\widehat{EFN}=180^0\)
Mà \(\widehat{EFN}+\widehat{EFB}=180^0\)
\(\Rightarrow\widehat{EMN}=\widehat{EFB}\)
Lại có tứ giác ABFM nội tiếp (A và F cùng nhìn BM dưới 1 góc vuông)
\(\Rightarrow\widehat{EFB}=\widehat{AMB}\) (cùng chắn AB)
\(\Rightarrow\widehat{EMN}=\widehat{AMB}\)
\(\Rightarrow\Delta_VAMB=\Delta_VHMB\left(ch-gn\right)\)
\(\Rightarrow AM=HM\)
Đồng thời suy ra \(AB=BH\Rightarrow BH=BC\) (do AB=BC)
Theo Pitago: \(\left\{{}\begin{matrix}HN=\sqrt{BN^2-BH^2}\\CN=\sqrt{BN^2-BC^2}\end{matrix}\right.\) \(\Rightarrow CN=HN\)
\(\Rightarrow AM+CN=MH+NH=MN\)
\(\Rightarrow MD+DN+MN=MD+DN+AM+CN=AD+CD=2a\)
Pitago: \(MN^2=DM^2+DN^2\ge\dfrac{1}{2}\left(DM+DN\right)^2\Rightarrow MN\ge\dfrac{\sqrt{2}}{2}\left(DM+DN\right)\)
\(\Rightarrow2a-\left(DM+DN\right)\ge\dfrac{\sqrt{2}}{2}\left(DM+DN\right)\)
\(\Rightarrow2a\ge\left(\dfrac{2+\sqrt{2}}{2}\right)\left(DM+DN\right)\ge\left(2+\sqrt{2}\right).\sqrt{DM.DN}\)
\(\Rightarrow DM.DN\le\left(6-4\sqrt{2}\right)a^2\)
\(\Rightarrow S_{MDN}=\dfrac{1}{2}DM.DN\le\left(3-2\sqrt{2}\right)a^2\)
Dấu "=" xảy ra khi \(DM=DN=\left(\sqrt{6}-\sqrt{2}\right)a\)

a) Xét hình thang ABCD(AB//CD) có
M là trung điểm của AD(gt)
N là trung điểm của BC(gt)
Do đó: MN là đường trung bình của hình thang ABCD(Định nghĩa đường trung bình của hình thang)
Suy ra: MN//AB//DC và \(MN=\dfrac{AB+CD}{2}\)(Định lí 4 về đường trung bình của hình thang)
hay \(MN=\dfrac{3+5}{2}=\dfrac{8}{2}=4\left(cm\right)\)
b) Ta có: AD//BE(gt)
AD\(\perp\)DC(gt)
Do đó: BE\(\perp\)DC(Định lí 2 từ vuông góc tới song song)
Xét tứ giác ABED có
\(\widehat{BAD}=90^0\)(gt)
\(\widehat{ADE}=90^0\)(gt)
\(\widehat{BED}=90^0\)(cmt)
Do đó: ABED là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

a: Xét ΔABC có
M là trung điểm của AC
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AB
hay AMNB là hình thang
mà \(\widehat{MAB}=90^0\)
nên AMNB là hình thang vuông

Câu hỏi của pham trung thanh - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo lời giải tại link trên nhé.

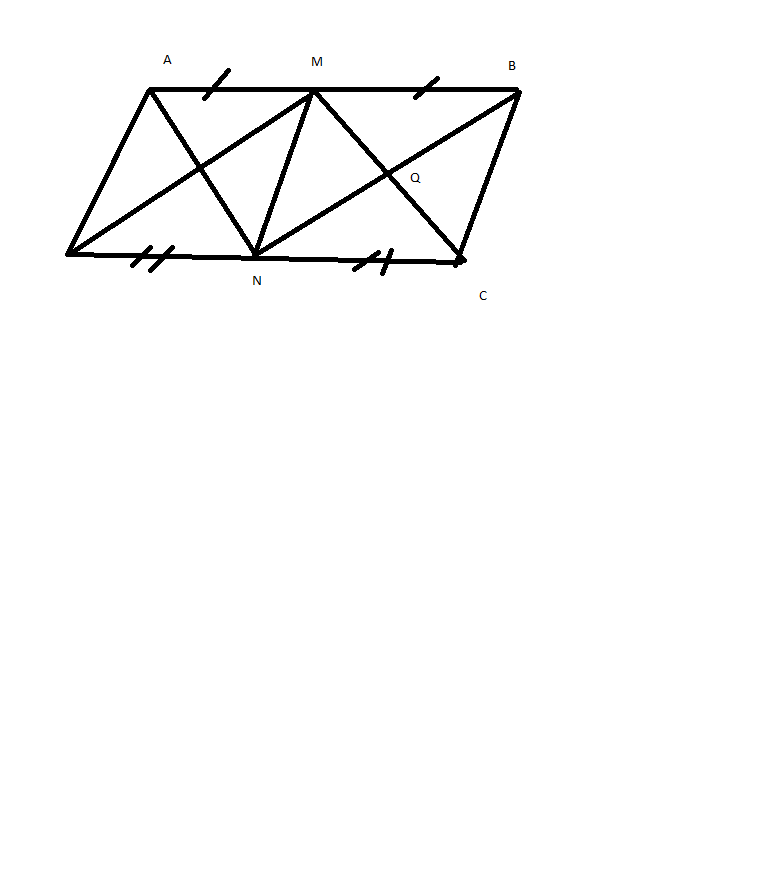
a) Vì ABCD là hình bình hành nên
AB=CD=2a, AD=BC=a
ta có: M,N là trung điểm của AB và CD
=> DN=1/2CD=a
=> AD=DN
Vậy tam giác ADN cân tại D(đpcm)
=> DAN=DNA
b) Ta có: AB//CD => AND=MAN(So le trong)
=> DAN=MAN
=>AN là tia phân giác của góc BAD



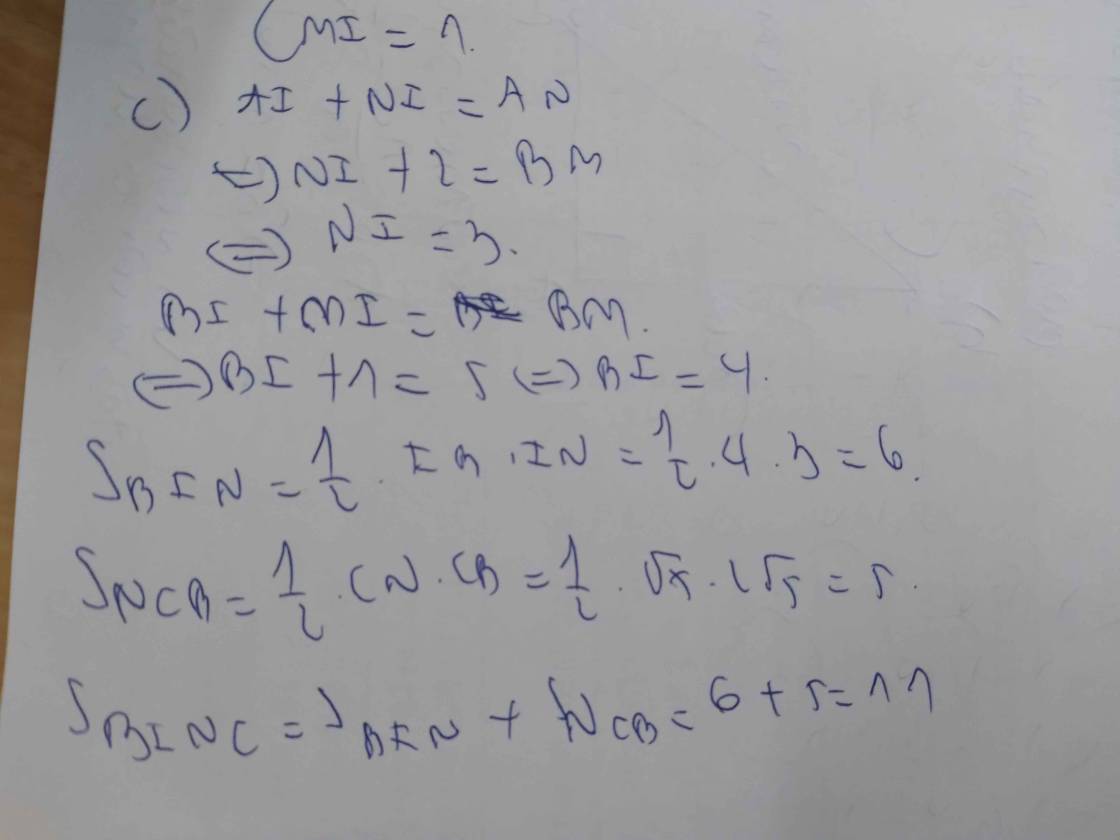
1: Ta có: \(AM=MD=\dfrac{AD}{2}\)
\(DN=NC=\dfrac{DC}{2}\)
mà AD=DC
nên AM=MD=DN=NC
Xét ΔADN vuông tại D và ΔBAM vuông tại A có
AD=BA
DN=AM
Do đó: ΔADN=ΔBAM
=>\(\widehat{AND}=\widehat{BMA}\)
=>\(\widehat{BMA}+\widehat{MAI}=90^0\)
=>AN\(\perp\)BM tại I
2: \(AM=\dfrac{AD}{2}=\dfrac{2\sqrt{5}}{2}=\sqrt{5}\left(cm\right)\)
ΔAMB vuông tại A
=>\(AM^2+AB^2=BM^2\)
=>\(BM=\sqrt{\left(2\sqrt{5}\right)^2+\left(\sqrt{5}\right)^2}=5\left(cm\right)\)
Xét ΔAMB vuông tại A có AI là đường cao
nên \(\left\{{}\begin{matrix}MI\cdot MB=MA^2\\AI\cdot MB=AM\cdot AB\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}MI\cdot5=\left(\sqrt[]{5}\right)^2=5\\AI\cdot5=2\sqrt{5}\cdot5=10\end{matrix}\right.\)
=>MI=1(cm); AI=10/5=2(cm)
3: MI+IB=MB
=>IB+1=5
=>IB=4(cm)
ΔAIB vuông tại I
=>\(S_{AIB}=\dfrac{1}{2}\cdot AI\cdot IB=\dfrac{1}{2}\cdot1\cdot4=2\left(cm^2\right)\)
ΔADN vuông tại D
=>\(S_{ADN}=\dfrac{1}{2}\cdot2\sqrt{5}\cdot\sqrt{5}=5\left(cm^2\right)\)
ABCD là hình vuông
=>\(S_{ABCD}=AB\cdot AD=2\sqrt{5}\cdot2\sqrt{5}=20\left(cm^2\right)\)
Ta có: \(S_{ABCD}=S_{AIB}+S_{ADN}+S_{NCBI}\)
=>\(S_{NIBC}+2+5=20\)
=>\(S_{NIBC}=13\left(cm^2\right)\)