tính nhanh có thể 1/2 -43/101+(-1/3)-1/6 cíu vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


155,9:4,5=34 dư 29
87,5:1,75=50
52:1,6=32,5
45,6:32=1,425

Giải:
\(\dfrac{1}{2}-\dfrac{43}{100}+\left(-\dfrac{1}{3}\right)-\dfrac{1}{6}\)
\(=-\dfrac{43}{100}+\dfrac{1}{2}+\left(-\dfrac{1}{3}\right)-\dfrac{1}{6}\)
\(=-\dfrac{43}{100}+\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\)
\(=-\dfrac{43}{100}+\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)\)
\(=-\dfrac{43}{100}+\left(\dfrac{3}{6}-\dfrac{2}{6}-\dfrac{1}{6}\right)\)
\(=-\dfrac{43}{100}+0=-\dfrac{43}{100}\)
Vậy ...

\(\frac{1}{2}-\frac{43}{101}+\frac{-1}{3}-\frac{1}{6}\)
\(=\left(\frac{1}{2}-\frac{1}{3}-\frac{1}{6}\right)+\left(-\frac{43}{101}\right)\)
\(=\frac{3-2-1}{6}+\frac{-43}{101}\)
\(=0+\frac{-43}{101}\)
\(=-\frac{43}{101}\)

\(\dfrac{1}{2}-\dfrac{43}{101}+\dfrac{-1}{3}-\dfrac{1}{6}\\ =\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)-\dfrac{43}{101}=0-\dfrac{43}{101}=-\dfrac{43}{101}\)

\(\left(1-\dfrac{1}{2}\right).\left(1-\dfrac{1}{3}\right).\left(1-\dfrac{1}{4}\right).....\left(1-\dfrac{1}{2004}\right)\)
\(=\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{3}{4}....\dfrac{2002}{2003}.\dfrac{2003}{2004}\)
\(=\dfrac{1}{2004}\)

\(11\div\left\{\frac{7}{8}-3\cdot\left[0,25\div\left(1\frac{1}{3}+2\cdot\frac{1}{3}\right)\right]\right\}\)
\(=11\div\left\{\frac{7}{8}-3\cdot\left[\frac{1}{4}\div\left(\frac{4}{3}+2\cdot\frac{1}{3}\right)\right]\right\}\)
\(=11\div\left\{\frac{7}{8}-3\cdot\left[\frac{1}{4}\div\left(\frac{4}{3}+\frac{2}{3}\right)\right]\right\}\)
\(=11\div\left\{\frac{7}{8}-3\cdot\left[\frac{1}{4}\div2\right]\right\}\)
\(=11\div\left\{\frac{7}{8}-3\cdot\frac{1}{8}\right\}\)
\(=11\div\left\{\frac{7}{8}-\frac{3}{8}\right\}\)
\(=11\div\frac{1}{2}\)
\(=22\)
b) 101*789 + 456*128 - 789 + 912*436
= 789*100 + 456*128 + 912*436
= 789*100 + 912*64 + 912*436
= 789*100 + 912*500
= 100*(789 + 912*5)
= 100*5349
= 534900

A = \(\dfrac{3^{100}.\left(-2\right)+3^{101}}{\left(-3\right)^{101}-3^{100}}\)
A = \(\dfrac{3^{100}.\left(-2\right)+3^{100}.3}{\left(-3\right)^{100}.\left(-3\right)-3^{100}}\)
A = \(\dfrac{3^{100}.\left(-2+3\right)}{3^{100}.\left(-3\right)-3^{100}}\)
A = \(\dfrac{3^{100}.1}{3^{100}.\left(-3-1\right)}\)
A = \(\dfrac{3^{100}}{3^{100}}\) . \(\dfrac{1}{-4}\)
A = - \(\dfrac{1}{4}\)
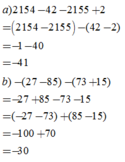

\(\dfrac{1}{2}-\dfrac{43}{101}+\left(-\dfrac{1}{3}\right)-\dfrac{1}{6}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}+\left(-\dfrac{43}{101}\right)\)
\(=0+\left(-\dfrac{43}{101}\right)\)
\(=-\dfrac{43}{101}\)
\(\dfrac{1}{2}-\dfrac{43}{101}+\left(-\dfrac{1}{3}\right)-\dfrac{1}{6}\\ =\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)-\dfrac{43}{101}\\ =\left(\dfrac{3}{6}-\dfrac{2}{6}-\dfrac{1}{6}\right)-\dfrac{43}{101}\\ =\dfrac{0}{6}-\dfrac{43}{101}\\ =-\dfrac{43}{101}\)