Giá trị của biểu thức : Cho 1/a^150 < (1/5)^225 . Giá trị số nguyên dương a nhỏ nhất là :
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a; A = \(\dfrac{1}{15}\) \(\times\) \(\dfrac{225}{x+2}\) + \(\dfrac{3}{14}\) \(\times\) \(\dfrac{196}{3x+6}\) (đk \(x\) ≠ - 2)
A = \(\dfrac{15}{x+2}\) + \(\dfrac{3\times14}{3\times\left(x+2\right)}\)
A = \(\dfrac{15}{x+2}\) + \(\dfrac{14}{x+2}\)
A = \(\dfrac{29}{x+2}\)
b; A = \(\dfrac{29}{x+2}\) (-2 ≠ \(x\) \(\in\) Z)
A \(\in\) Z ⇔ 29 ⋮ \(x\) + 2
\(x\) + 2 \(\in\) Ư(29) = {-29; - 1; 1; 29}
Lập bảng ta có:
| \(x\) + 2 | - 29 | - 1 | 1 | 29 |
| \(x\) | -31 | -3 | -1 | 27 |
Theo bảng trên ta có: \(x\) \(\in\) {- 31; -3; -1; 27}
Vậy \(x\) \(\in\) {-31; -3; -1; 27}

Làm khâu rút gọn thôi
\(=\frac{15}{x+2}+\frac{42}{3x+6}\)
\(=\frac{15}{x+2}+\frac{42}{3\left(x+2\right)}\)
\(=\frac{3.15+42}{3\left(x+2\right)}\)
\(=\frac{87}{3\left(x+2\right)}\)
\(=\frac{29}{x+2}\)
Câu b có phải để tử chia hết cho mẫu không nhỉ? Không chắc thôi để ngkh làm

\(C=\frac{2\left(x-1\right)^2+1}{\left(x-1\right)^2+2}\)
a, Ta thấy \(\left(x-1\right)^2\ge0\forall x\Rightarrow\hept{\begin{cases}2\left(x-1\right)^2+1\ge1>0\\\left(x-1\right)^2+2\ge2>0\end{cases}}\)
\(\Rightarrow C>0\forall x\)(đpcm)
b, \(C=\frac{2\left(x-1\right)^2+1}{\left(x-1\right)^2+2}=\frac{2\left(x-1\right)^2+4-3}{\left(x-1\right)^2+2}=2-\frac{3}{\left(x-1\right)^2+2}\)
\(C\in Z\Leftrightarrow2-\frac{3}{\left(x-1\right)^2+2}\in Z\)
\(\Leftrightarrow\frac{3}{\left(x-1\right)^2+2}\in Z\)Lại do \(\left(x-1\right)^2+2\ge2\)
\(\Leftrightarrow\left(x-1\right)^2+2\inƯ\left(3\right)=\left\{3\right\}\)
\(\Leftrightarrow\left(x-1\right)^2\in\left\{1\right\}\)
\(\Leftrightarrow x\in\left\{0\right\}\)
....
c, \(C=2-\frac{3}{\left(x-1\right)^2+2}\)
Ta có : \(\left(x-1\right)^2+2\ge2\Rightarrow\frac{3}{\left(x-1\right)^2+2}\le\frac{3}{2}\)
\(\Rightarrow C=2-\frac{3}{\left(x-1\right)^2+2}\ge2-\frac{3}{2}=\frac{1}{2}\)
Dấu "=" xảy ra khi \(x-1=0\Leftrightarrow x=1\)
:33

A = \(\dfrac{2x-1}{x+2}\)
a, A là phân số ⇔ \(x\) + 2 # 0 ⇒ \(x\) # -2
b, Để A là một số nguyên thì 2\(x-1\) ⋮ \(x\) + 2
⇒ 2\(x\) + 4 - 5 ⋮ \(x\) + 2
⇒ 2(\(x\) + 2) - 5 ⋮ \(x\) + 2
⇒ 5 ⋮ \(x\) + 2
⇒ \(x\) + 2 \(\in\) { -5; -1; 1; 5}
⇒ \(x\) \(\in\) { -7; -3; -1; 3}
c, A = \(\dfrac{2x-1}{x+2}\)
A = 2 - \(\dfrac{5}{x+2}\)
Với \(x\) \(\in\) Z và \(x\) < -3 ta có
\(x\) + 2 < - 3 + 2 = -1
⇒ \(\dfrac{5}{x+2}\) > \(\dfrac{5}{-1}\) = -5 ⇒ - \(\dfrac{5}{x+2}\)< 5
⇒ 2 - \(\dfrac{5}{x+2}\) < 2 + 5 = 7 ⇒ A < 7 (1)
Với \(x\) > -3; \(x\) # - 2; \(x\in\) Z ⇒ \(x\) ≥ -1 ⇒ \(x\) + 2 ≥ -1 + 2 = 1
\(\dfrac{5}{x+2}\) > 0 ⇒ - \(\dfrac{5}{x+2}\) < 0 ⇒ 2 - \(\dfrac{5}{x+2}\) < 2 (2)
Với \(x=-3\) ⇒ A = 2 - \(\dfrac{5}{-3+2}\) = 7 (3)
Kết hợp (1); (2) và(3) ta có A(max) = 7 ⇔ \(x\) = -3

Chọn đáp án B
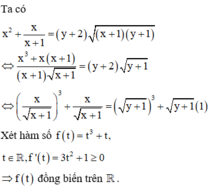
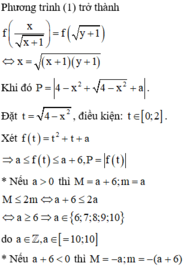
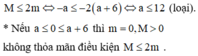
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.

A =15/x+2 + 14/x+2 = 29/x+2
b) x+2 là U(29) = { -1;1;-29;29}
=> x ={ -3;-1;-31;27}


\(\dfrac{1}{a^{150}}< \left(\dfrac{1}{5}\right)^{225}\\ \Rightarrow\left(\dfrac{1}{a}\right)^{150}< \left(\dfrac{1}{5}\right)^{225}\\ \Rightarrow\left[\left(\dfrac{1}{a}\right)^2\right]^{75}< \left[\left(\dfrac{1}{5}\right)^3\right]^{75}\\ \Rightarrow\left(\dfrac{1}{a}\right)^2< \left(\dfrac{1}{5}\right)^3\\ \Rightarrow\dfrac{1}{a^2}< \dfrac{1}{5^3}\\ \Rightarrow a^2>5^3\\ \Rightarrow a^2>125\)
Mà: a là số nguyên dương nhỏ nhất
Vậy: a = 12