tìm x ko âm bt
\(\sqrt{x}=1-\sqrt{3}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{x}=-3\left(VLý.do\sqrt{x}\ge0\forall x\right)\)
Vậy \(S=\varnothing\)

a)
\(\sqrt{x}=4\Rightarrow x=4^2=16\)
c) \(x\in\varnothing\)
e) \(\sqrt{x}=6,25\Rightarrow x=\left(6,25\right)^2=39,0625\)
b) \(\sqrt{x}=\sqrt{7}\Rightarrow x=7\)
d) \(\sqrt{x}=0\Rightarrow x=0\)
Cách đánh đề độc lạ ghê:v
a: =>x=16
b: =>x=7
c: =>x thuộc rỗng
d: =>x=0
e: =>x=(25/4)^2=625/16

\(2x-3\sqrt{x}+2=2\left(\sqrt{x}-\dfrac{3}{4}\right)^2+\dfrac{7}{8}\ge\dfrac{7}{8}\)
\(\Rightarrow\dfrac{1}{2x-3\sqrt{x}+2}\le\dfrac{1}{\dfrac{7}{8}}=\dfrac{8}{7}\)
\(\Rightarrow\dfrac{-1}{2x-3\sqrt{x}+2}\ge-\dfrac{8}{7}\)
\(A_{min}=-\dfrac{8}{7}\) khi \(x=\dfrac{9}{16}\)
Ta thấy:\(2x-3\sqrt{x}+2=2\left(x-\dfrac{3}{2}\sqrt{x}+1\right)\)\(=2\left(x-2.\dfrac{3}{4}\sqrt{x}+\dfrac{9}{16}+\dfrac{7}{16}\right)=2\left(\sqrt{x}-\dfrac{3}{4}\right)^2+\dfrac{7}{8}\)
Vì \(2\left(\sqrt{x}-\dfrac{3}{4}\right)^2\ge0\) với \(\forall x\ge0\) nên \(2\left(\sqrt{x}-\dfrac{3}{4}\right)^2+\dfrac{7}{8}\ge\dfrac{7}{8}\)với \(\forall x\ge0\)
\(\Rightarrow\dfrac{1}{2x-3\sqrt{x}+2}\le\dfrac{7}{8}\)với \(\forall x\ge0\)
\(\Rightarrow A=\dfrac{-1}{2x-3\sqrt{x}+2}\ge-\dfrac{7}{8}\)với \(\forall x\ge0\)
Dấu "=" xảy ra khi và chỉ khi \(\sqrt{x}-\dfrac{3}{4}=0\Leftrightarrow\sqrt{x}=\dfrac{3}{4}\Leftrightarrow x=\dfrac{9}{16}\)
xin lỗi nha bài này tui gửi nhầm lên đây nên đừng nói tui tự làm tự giải kiếm điểm nhá

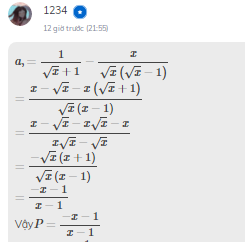
Mk ra đáp án khác với đáp án ủa bn nên bn bào sai chứ j, thật ra cả 2 đáp án đều giống nhau, do biến đổi dấu nên trở thành 2 đáp án khác nhau thôi :V
để mk lm lại phần đáp án của mk ra giống đáp án của bn nek :V
\(a,\)\(P=\dfrac{-x-1}{x-1}\)
\(\Rightarrow\dfrac{-\left(-x-1\right)}{-\left(x-1\right)}=\dfrac{x-1}{-x+1}=\dfrac{x-1}{1-x}\)
Còn câu b thì hôm qua bn ghi là \(x=\dfrac{1}{\sqrt{2}}\) chứ có pk là \(1\sqrt{2}\) đou >:V
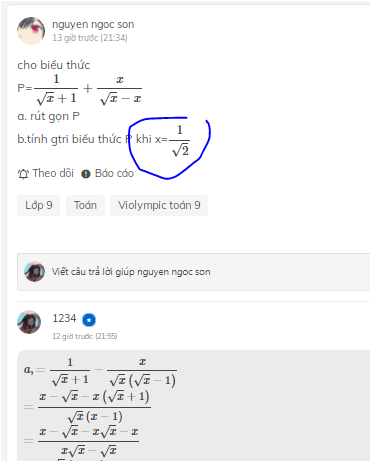
\(b,\)Thay \(x=1\sqrt{2}\) vào \(P\) ta có :
\(P=\dfrac{x-1}{1-x}\)
\(P=\dfrac{1\sqrt{2}-1}{1-1\sqrt{2}}=3+2\sqrt{2}\)

ĐKXĐ: \(x>0;x\ne1\)
\(A=\left(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{2\left(\sqrt{x}+1\right)}{x\left(\sqrt{x}+1\right)}-\dfrac{2-x}{x\left(\sqrt{x}+1\right)}\right)\)
\(=\left(\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{x+2\sqrt{x}}{x\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{\left(x+2\sqrt{x}\right).x.\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\left(x+2\sqrt{x}\right)}=\dfrac{x}{\sqrt{x}-1}\)
b.
\(x=4+2\sqrt{3}=\left(\sqrt{3}+1\right)^2\Rightarrow\sqrt{x}=\sqrt{3}+1\)
\(\Rightarrow A=\dfrac{4+2\sqrt{3}}{\sqrt{3}+1-1}=\dfrac{4+2\sqrt{3}}{\sqrt{3}}=\dfrac{6+4\sqrt{3}}{3}\)
c.
Để \(\sqrt{A}\) xác định \(\Rightarrow\sqrt{x}-1>0\Rightarrow x>1\)
Ta có:
\(\sqrt{A}=\sqrt{\dfrac{x}{\sqrt{x}-1}}=\sqrt{\dfrac{x}{\sqrt{x}-1}-4+4}=\sqrt{\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-1}+4}\ge\sqrt{4}=2\)
Dấu "=" xảy ra khi \(\sqrt{x}-2=0\Rightarrow x=4\)

\(a,\) ta có :
\(\Leftrightarrow\left\{{}\begin{matrix}A=\sqrt{3}+\sqrt{2^2.3}-\sqrt{3^2.3}-\sqrt{6^2}\\A=\sqrt{3}+2\sqrt{3}-3\sqrt{3}-6\\A=\sqrt{3}.\left(1+2-3\right)-6\\A=-6\end{matrix}\right.\)
\(\Rightarrow A=-6\) . vậy \(A=9\sqrt{5}\)
__________________________________________________________
\(b,\) với \(x>0\) và \(x\ne1\) . ta có :
\(B=\dfrac{2}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}}+\dfrac{3\sqrt{x}-5}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow B=\dfrac{2\sqrt{x}-\left(\sqrt{x}-1\right)+3\sqrt{x}-5}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow B=\dfrac{2\sqrt{x}-\sqrt{x}+1+3\sqrt{x}-5}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow B=\dfrac{4\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow\) \(B=\dfrac{4\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow B=\dfrac{4}{\sqrt{x}}\)
vậy với \(x>0\) \(;\) \(x\ne1\) thì \(B=\dfrac{4}{\sqrt{x}}\)
để \(B=2\) thì \(\dfrac{4}{\sqrt{x}}=2\Leftrightarrow\sqrt{x}=2\Leftrightarrow x=4\left(tm\right)\)
vậy để \(B=2\) thì \(x=4\)

1) \(A=\dfrac{\left(\sqrt{x}+1\right)^2+\left(\sqrt{x}-1\right)^2-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(2x-2\sqrt{x}\right)-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(2\sqrt{x}-1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
b) \(A=\dfrac{2\sqrt{9}-1}{\sqrt{9}+1}=\dfrac{5}{4}\)
c) \(A=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}< 1\Rightarrow2\sqrt{x}-1< \sqrt{x}+1\Rightarrow\sqrt{x}< 2\Rightarrow x< 4\)
\(1,A=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ A=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(2\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\\ 2,x=9\Leftrightarrow A=\dfrac{6-1}{3+1}=\dfrac{5}{4}\\ 3,A< 1\Leftrightarrow\dfrac{2\sqrt{x}-1-\sqrt{x}-1}{\sqrt{x}+1}< 0\\ \Leftrightarrow\dfrac{\sqrt{x}-2}{\sqrt{x}+1}< 0\Leftrightarrow\sqrt{x}-2< 0\left(\sqrt{x}+1>0\right)\\ \Leftrightarrow x< 4\Leftrightarrow0\le x< 4\)

a: Ta có: \(\sqrt{x}< 3\)
nên \(0\le x< 9\)
b: Ta có: \(\sqrt{4x+16}+\sqrt{x+4}+2\sqrt{9x+36}=35\)
\(\Leftrightarrow2\sqrt{x+4}+\sqrt{x+4}+6\sqrt{x+4}=35\)
\(\Leftrightarrow\sqrt{x+4}=\dfrac{35}{9}\)
\(\Leftrightarrow x+4=\dfrac{1225}{81}\)
hay \(x=\dfrac{901}{81}\)
a) \(\sqrt{x}< 3\Rightarrow x< 9\)
b) \(\sqrt{4x+16}+\sqrt{x+4}+2\sqrt{9x+36}=35\)
\(\Rightarrow2\sqrt{x+4}+\sqrt{x+4}+6\sqrt{x+4}=35\)
\(\Rightarrow\sqrt{x+4}=\dfrac{35}{9}\)
\(\Rightarrow x+4=\dfrac{1225}{81}\)
\(\Rightarrow x=\dfrac{901}{81}\)
c) \(\sqrt{x+2\sqrt{x-1}}=3\)
\(\Rightarrow\sqrt{\left(x-1\right)+2\sqrt{x-1}+1}=3\)
\(\Rightarrow\sqrt{\left(x-1+1\right)^2}=3\)
\(\Rightarrow\sqrt{x^2}=3\)
\(\Rightarrow\left|x\right|=3\) \(\Rightarrow\left\{{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)
\(\sqrt{x}=1-\sqrt{3}\)
Nhận xét:
\(\sqrt{3}>\sqrt{1}=1\)
\(\Rightarrow1-\sqrt{3}< 0\)
\(\Rightarrow\sqrt{x}< 0\) (vô lí)
Vậy không tìm được giá trị x thoả mãn đề bài