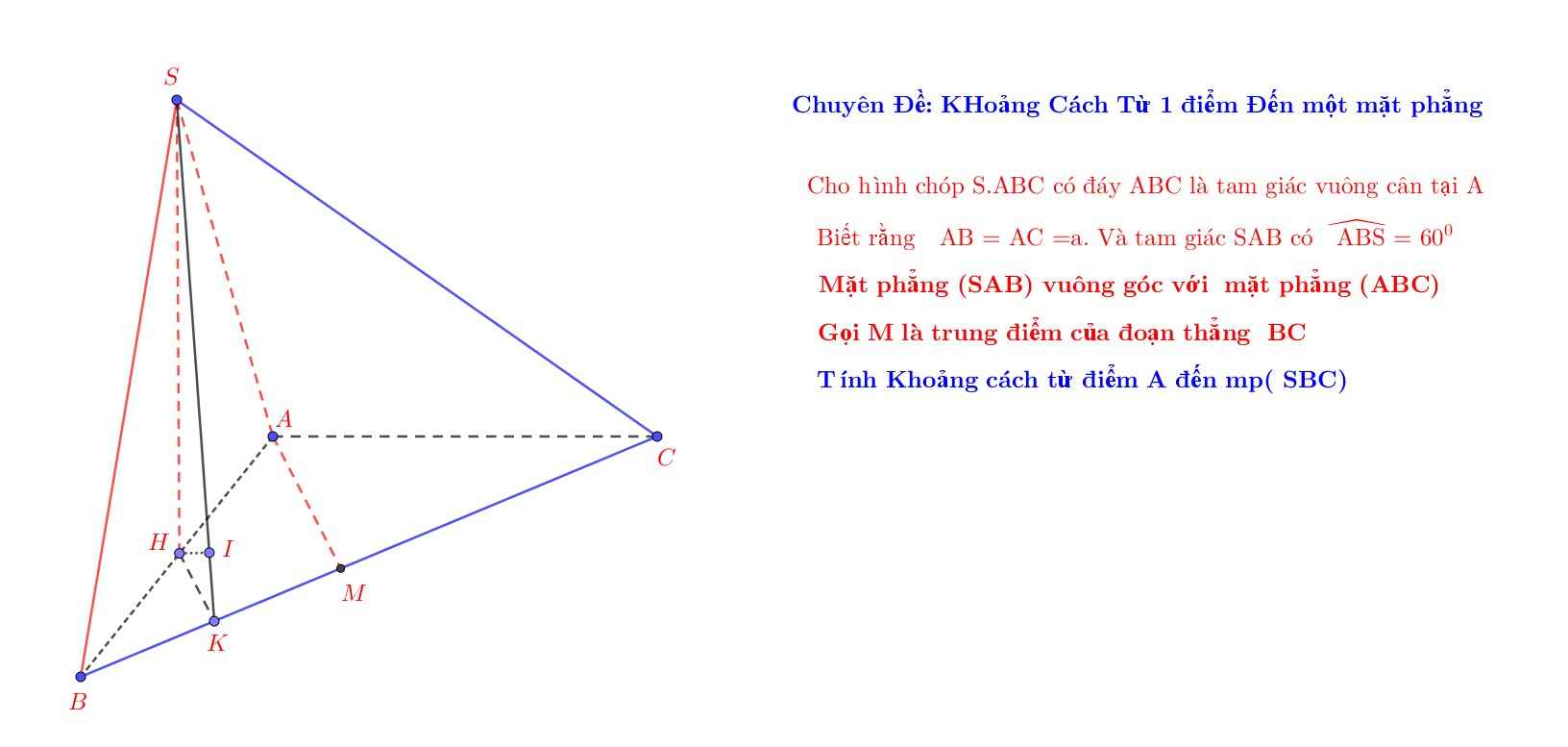
Cho hình chóp SABC có đáy là tam giác vuông cân tại A . Biết AB =a , SA vuông góc với đáy và SB tạo với đáy góc 45 độ . Tính khoảng cách từ A đến mặt phẳng (SBC)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hình bạn tự vẽ nha mình biếng á chứ khog có j đou=)
Ta có : \(\left\{{}\begin{matrix}CA\perp AB\\\left(ABC\right)\perp\left(SAB\right)\\\left(ABC\right)\cap\left(SAB\right)=AB\end{matrix}\right.\) \(\Rightarrow CA\perp\left(SAB\right)\)
Kẻ \(AK\perp SB\) và \(AH\perp CK\) tại H.
Ta có : \(\left\{{}\begin{matrix}SB\perp AK\\SB\perp CA\end{matrix}\right.\) \(\Rightarrow SB\perp\left(ACK\right)\Rightarrow SB\perp AH\)
Do : \(\left\{{}\begin{matrix}AH\perp CK\\AH\perp SB\end{matrix}\right.\) \(\Rightarrow AH\perp\left(SBC\right)\Rightarrow d\left(A;\left(SBC\right)\right)=AH\)
Xét t/g ABK , ta có : AK = AB
=> \(sin\widehat{ABK}=\alpha sin60^o=\dfrac{a\sqrt{3}}{2}\)
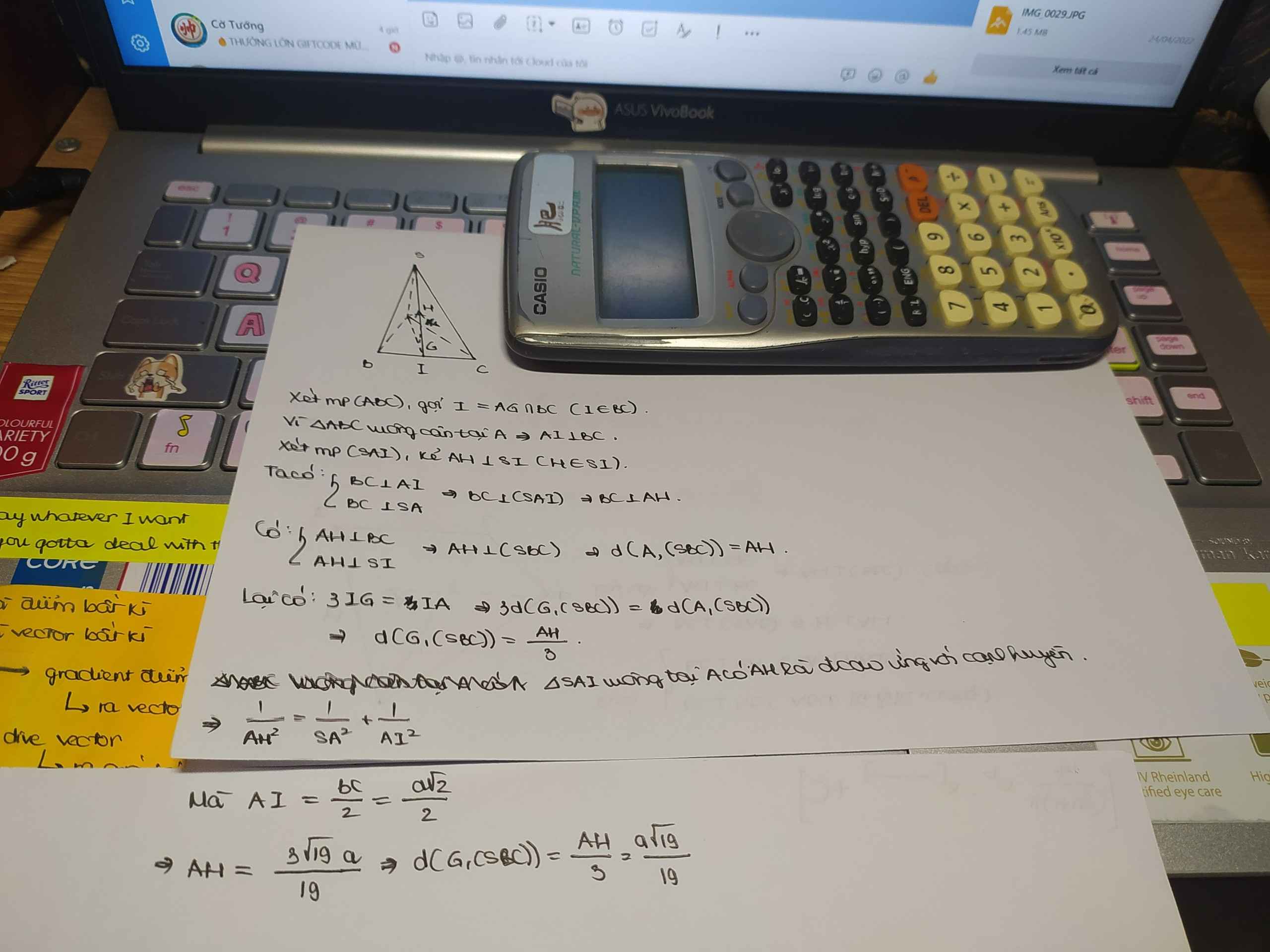
Xét t/g ACK , ta có : \(\dfrac{1}{AH^2}=\dfrac{1}{AK^2}+\dfrac{1}{AC^2}=\dfrac{7}{3a^2}\Rightarrow AH=\dfrac{a\sqrt{21}}{7}\)

Kẻ A H ⊥ B C và A H ⊥ S I . Khi đó A H ⊥ S B C ⇒ d A , S B C = A H
Ta có A I = a 3 2 (do ∆ A B C đều cạnh a)
và
S B A B C = S B A ^ = 60 o ⇒ S A = A B . tan 60 = a 3
Vậy d A S B C = A H = S A . A I S A 2 + A I 2 = a 15 5
Đáp án A

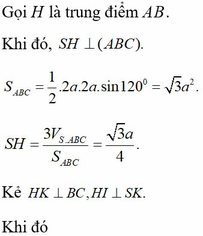
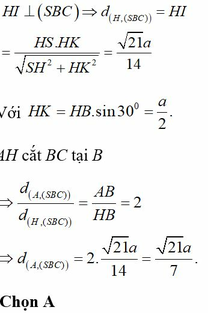
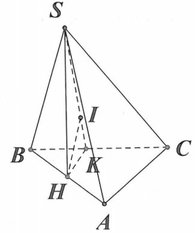
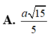
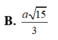
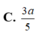
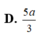
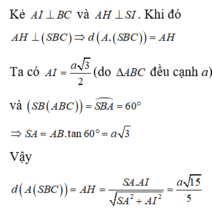

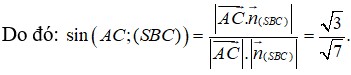
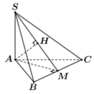
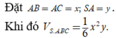
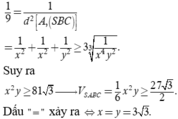
Kẻ AH\(\perp\)BC tại H, AK\(\perp\)SH tại K
\(\widehat{SB;\left(ABC\right)}=45^0\)
=>\(\widehat{BS;BA}=45^0\)
=>\(\widehat{SBA}=45^0\)
Xét ΔSAB vuông tại A có \(tanSBA=\dfrac{SA}{AB}\)
=>\(\dfrac{SA}{a}=tan45=1\)
=>SA=a
ΔABC vuông cân tại A
=>\(AB=AC=a\) và \(BC=\sqrt{AB^2+AC^2}=a\sqrt{2}\)
ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>\(AH=HB=HC=\dfrac{BC}{2}=\dfrac{a\sqrt{2}}{2}\)
Ta có: BC\(\perp\)AH
BC\(\perp\)SA
AH,SA cùng thuộc mp(SAH)
Do đó: BC\(\perp\)(SAH)
=>BC\(\perp\)AK
Ta có: AK\(\perp\)SH
AK\(\perp\)BC
SH,BC cùng thuộc mp(SBC)
Do đó: AK\(\perp\)(SBC)
=>AK là khoảng cách từ A đến mp(SBC)
ΔSAH vuông tại A
=>\(SH^2=SA^2+AH^2=a^2+\left(\dfrac{a\sqrt{2}}{2}\right)^2=a^2+\dfrac{1}{2}a^2=\dfrac{3}{2}a^2\)
=>\(SH=\dfrac{a\sqrt{6}}{2}\)
Xét ΔSAH vuông tại A có AK là đường cao
nên \(AK\cdot SH=SA\cdot AH\)
=>\(AK\cdot\dfrac{a\sqrt{6}}{2}=a\cdot\dfrac{a\sqrt{2}}{2}\)
=>\(AK\cdot\sqrt{6}=a\sqrt{2}\)
=>\(AK=a\sqrt{\dfrac{2}{6}}=a\sqrt{\dfrac{1}{3}}=\dfrac{a\sqrt{3}}{3}\)