K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 7 2021
\(BC=AB\sqrt{2}=a\sqrt{2}\)
\(SB=\sqrt{SC^2+BC^2}=a\sqrt{3}\) ; \(SA=\sqrt{SC^2+AC^2}=a\sqrt{2}\)
\(V_{SBAC}=\dfrac{1}{3}SC.\dfrac{1}{2}AB^2=\dfrac{a^3}{6}\)
\(\dfrac{V_{SCEF}}{V_{SABC}}=\dfrac{SF}{SB}.\dfrac{SE}{SA}=\left(\dfrac{SC}{SB}\right)^2\left(\dfrac{SC}{SA}\right)^2=\left(\dfrac{a}{a\sqrt{3}}\right)^2.\left(\dfrac{a}{a\sqrt{2}}\right)^2=\dfrac{1}{6}\)
\(\Rightarrow V_{SCEF}=\dfrac{1}{6}.\dfrac{a^3}{6}=\dfrac{a^3}{36}\)
7 tháng 7 2021
Kết quả không có a³/18
Chỉ có là A)a³/6. B)a³/16
C)a³/26. D)a³/36 thôi ạ
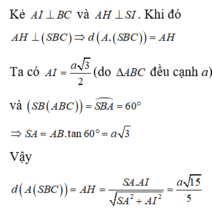
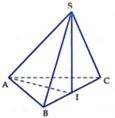

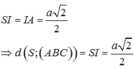
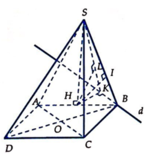

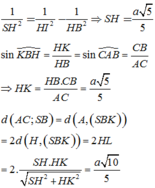
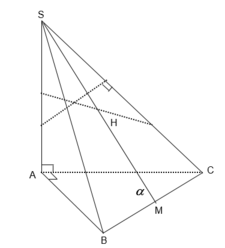

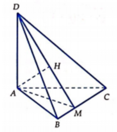


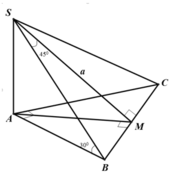

Kẻ AH\(\perp\)BC tại H, AK\(\perp\)SH tại K
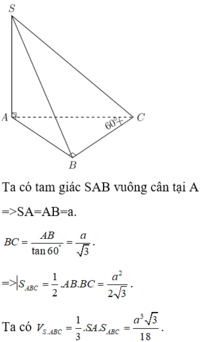
\(\widehat{SB;\left(ABC\right)}=45^0\)
=>\(\widehat{BS;BA}=45^0\)
=>\(\widehat{SBA}=45^0\)
Xét ΔSAB vuông tại A có \(tanSBA=\dfrac{SA}{AB}\)
=>\(\dfrac{SA}{a}=tan45=1\)
=>SA=a
ΔABC vuông cân tại A
=>\(AB=AC=a\) và \(BC=\sqrt{AB^2+AC^2}=a\sqrt{2}\)
ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>\(AH=HB=HC=\dfrac{BC}{2}=\dfrac{a\sqrt{2}}{2}\)
Ta có: BC\(\perp\)AH
BC\(\perp\)SA
AH,SA cùng thuộc mp(SAH)
Do đó: BC\(\perp\)(SAH)
=>BC\(\perp\)AK
Ta có: AK\(\perp\)SH
AK\(\perp\)BC
SH,BC cùng thuộc mp(SBC)
Do đó: AK\(\perp\)(SBC)
=>AK là khoảng cách từ A đến mp(SBC)
ΔSAH vuông tại A
=>\(SH^2=SA^2+AH^2=a^2+\left(\dfrac{a\sqrt{2}}{2}\right)^2=a^2+\dfrac{1}{2}a^2=\dfrac{3}{2}a^2\)
=>\(SH=\dfrac{a\sqrt{6}}{2}\)
Xét ΔSAH vuông tại A có AK là đường cao
nên \(AK\cdot SH=SA\cdot AH\)
=>\(AK\cdot\dfrac{a\sqrt{6}}{2}=a\cdot\dfrac{a\sqrt{2}}{2}\)
=>\(AK\cdot\sqrt{6}=a\sqrt{2}\)
=>\(AK=a\sqrt{\dfrac{2}{6}}=a\sqrt{\dfrac{1}{3}}=\dfrac{a\sqrt{3}}{3}\)