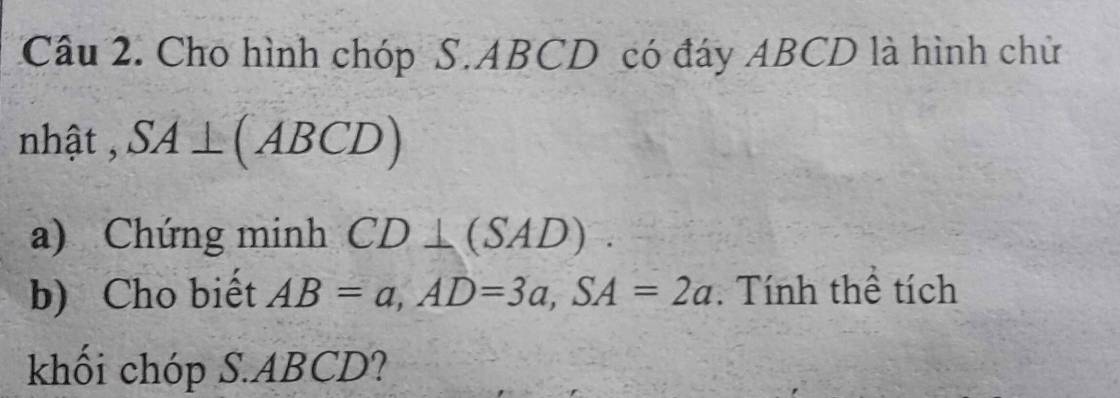thanks nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
I3
23 tháng 11 2021
ƯC của(−15;+20) là: {±1;±5}
đây là theo hiểu biết của mk thôi nha, ko chép ai đâu^^
BN
0
3 tháng 12 2023
\(x^3-y^3-z^3=3xyz\)
=>\(\left(x-y\right)^3-z^3+3xy\left(x-y\right)-3xyz=0\)
=>\(\left(x-y-z\right)\left[\left(x-y\right)^2+z\left(x-y\right)+z^2\right]+3xy\left(x-y-z\right)=0\)
=>\(\left(x-y-z\right)\left[x^2-2xy+y^2+xz-zy+z^2+3xy\right]=0\)
=>\(\left(x-y-z\right)\left(x^2+y^2+z^2+xy+xz-yz\right)=0\)
=>\(\left(x-y-z\right)\left(2x^2+2y^2+2z^2+2xy+2xz-2yz\right)=0\)
=>\(\left(x-y-z\right)\left[\left(x^2+2xy+y^2\right)+\left(y^2-2yz+z^2\right)+\left(x^2+2xz+z^2\right)\right]=0\)
=>\(\left(x-y-z\right)\left[\left(x+y\right)^2+\left(y-z\right)^2+\left(x+z\right)^2\right]=0\)
=>\(\left[{}\begin{matrix}x-y-z=0\\\left(x+y\right)^2+\left(y-z\right)^2+\left(x+z\right)^2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=y+z\\y=z=-x\end{matrix}\right.\)
\(H=\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\left(1-\dfrac{z}{x}\right)\)
\(=\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}\cdot\dfrac{x-z}{x}\)
TH1: x=y+z
=>\(H=\dfrac{y-x}{y}\cdot\dfrac{x}{z}\cdot\dfrac{x-z}{x}\)
\(=\dfrac{y}{x}\cdot\dfrac{z}{x}\cdot\dfrac{y-x}{y}=\dfrac{y}{x}\cdot\dfrac{z}{x}\cdot\dfrac{-z}{y}=-1\)
TH2: y=z=-x
=>y+x+z=0(vô lý vì x,y,z đều dương)
Vậy: H=-1
NT
1
31 tháng 1 2024
55:
Chiều rộng mảnh vườn là \(56\cdot\dfrac{5}{8}=35\left(m\right)\)
Chu vi mảnh vườn là \(\left(56+35\right)\cdot2=182\left(m\right)\)
Diện tích mảnh vườn là \(56\cdot35=1960\left(m^2\right)\)
56:
Ngày thứ nhất trồng được \(56\cdot\dfrac{3}{8}=7\cdot3=21\left(cây\right)\)
Số cây còn lại cần trồng là:
56-21=35(cây)
Ngày 2 trồng được \(35\cdot\dfrac{4}{7}=20\left(cây\right)\)
NT
1
AH
Akai Haruma
Giáo viên
12 tháng 9 2021
Bạn không chụp hết đề nhưng mình đoán là tìm $m$ để hàm số đồng biến trên $\mathbb{R}$
Lời giải:
Để hàm số đồng biến trên $\mathbb{R}$ thì:
$y'=3mx^2-2(2m-1)x+(m-2)\geq 0, \forall x\in\mathbb{R}$
Điều này xảy ra khi:
\(\left\{\begin{matrix} 3m>0\\ \Delta'=(2m-1)^2-3m(m-2)\leq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m>0\\ (m+1)^2\leq 0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m>0\\ m=-1\end{matrix}\right.\) (vô lý)
Vậy không tồn tại $m$ để hs đồng biến trên $\mathbb{R}$
L
2
TP
19 tháng 6 2021
Bài 9.
BTKL: m hh đầu = mX => nX = mhh đầu : MX = (0,5.26 + 0,4.52 + 0,65.2) : 39 = 0,9 mol
nH2 phản ứng = nban đầu - nX = (0,5 + 0,4 + 0,65) - 0,9 = 0,65 mol => số mol H2 đã phản ứng (H2 hết)
Trong X, ta đặt số mol CH≡CH, CH≡C-CH=CH2; CH≡C-CH2-CH3 lần lượt là x, y, z.
+) x + y + z = nX – nY = 0,9 – 0,45 = 0,45 (1)
+) nAgNO3 = 2nC2H2 + nC4H4 + nC≡C-C-C => 2x + y + z = 0,7 (2)
+) BT liên kết π: 2nC2H2 bđ + 3nC4H4 bđ = nH2 pư + 2nC2H2 dư + 3nC4H4 dư + 2nC≡C-C-C + nBr2
=> 0,5.2 + 0,4.3 = 0,65 + 2x + 3y + 2z + 0,55 => 2x + 3y + 2z = 1 (3)
Từ (1), (2) và (3) => x = 0,25 mol; y = 0,1 mol; z = 0,1 mol
=> Kết tủa tạo thành: CAg≡CAg (0,25 mol); CAg≡C−CH=CH2 (0,1 mol); CAg≡C−CH2−CH3 (0,1 mol)
=> m kết tủa = 0,25.240 + 0,1.159 + 0,1.161 = 92g
=> Chọn B
TP
0
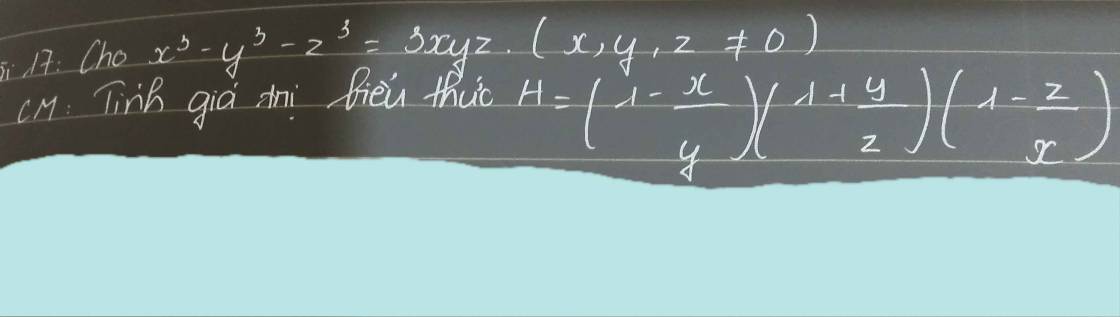
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow CD\perp\left(SAD\right)\)
b.
\(V=\dfrac{1}{3}SA.AB.AD=2a^3\)