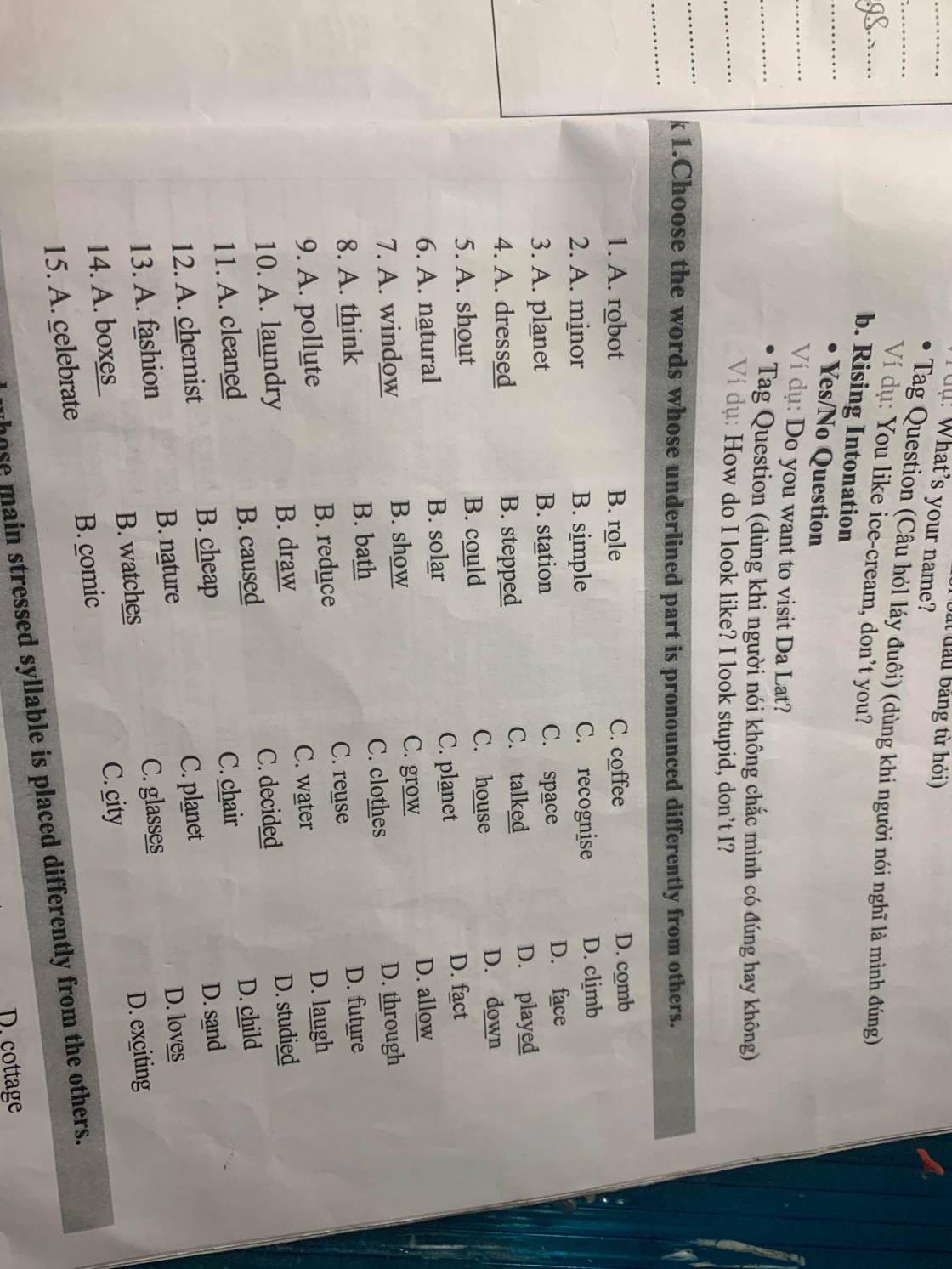
Giúp mình bài 1 với ah
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 4 2022
Bài 5:
-Áp dụng BĐT AM-GM ta có:
\(\dfrac{\left(a+b\right)^2}{4}\ge ab>a+b\)
\(\Rightarrow\left(a+b\right)^2>4\left(a+b\right)\)
\(\Leftrightarrow\left(a+b\right)^2-4\left(a+b\right)>0\)
\(\Leftrightarrow\left(a+b\right)\left(a+b-4\right)>0\)
\(\Leftrightarrow a+b-4>0\) (do \(a+b>0\))
\(\Leftrightarrow a+b>4\) (đpcm)
29 tháng 4 2022
Bài 4:
a) -△ABC có: AD là phân giác.
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{MB}{MC}\Rightarrow\dfrac{MB}{MC}=\dfrac{6}{8}=\dfrac{3}{4}\).
b) -△ABC và △MNC có: \(\widehat{BAC}=\widehat{NMC}=90^0;\widehat{ACB}\) là góc chung.
\(\Rightarrow\)△ABC∼△MNC (g-g).
c) -△ABC vuông tại A có: \(BC^2=AB^2+AC^2\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(\dfrac{MB}{MC}=\dfrac{AB}{AC}\Rightarrow\dfrac{MB}{AB}=\dfrac{MC}{AC}=\dfrac{MB+MC}{AB+AC}=\dfrac{BC}{AB+AC}\)
\(\Rightarrow MC=\dfrac{BC.AC}{AB+AC}=\dfrac{10.8}{6+8}=\dfrac{40}{7}\left(cm\right)\)
△ABC∼△MNC\(\Rightarrow\dfrac{S_{ABC}}{S_{MNC}}=\left(\dfrac{AC}{MC}\right)^2=\dfrac{8}{\dfrac{40}{7}}=\dfrac{7}{5}\)
\(\Rightarrow S_{MNC}=\dfrac{5}{7}S_{ABC}=\dfrac{5}{7}.\dfrac{1}{2}.6.8=15\left(cm^2\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 5 2021
Phương trình \(\Delta\) có dạng:
\(y=m\left(x+1\right)-2\Leftrightarrow y=mx+m-2\)
Phương trình hoành độ giao điểm (P) và \(\Delta\):
\(-\dfrac{1}{2}x^2=mx+m-2\Leftrightarrow x^2+2mx+2m-4=0\) (1)
\(\Delta'=m^2-2m+4=\left(m-1\right)^2+3>0\) ; \(\forall m\)
\(\Rightarrow\) (1) luôn có 2 nghiệm pb với mọi m hay (P) luôn cắt \(\Delta\) tại 2 điểm pb
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=-2m\\x_Ax_B=2m-4\end{matrix}\right.\)
Đặt \(A=x_A^2x_B+x_Ax_B^2=x_Ax_B\left(x_A+x_B\right)\)
\(A=-2m\left(2m-4\right)=-4m^2+8m=-4\left(m-1\right)^2+4\le4\)
\(A_{max}=4\) khi \(m=1\)
19 tháng 8 2021
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=9\cdot25=225\\AC^2=16\cdot25=400\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{15}{25}=\dfrac{3}{5}\)
\(\Leftrightarrow\widehat{C}\simeq37^0\)
\(\Leftrightarrow\widehat{B}=53^0\)
14 tháng 7 2023
Bài 3 :
\(BC=HC+HB=16+9=25\left(cm\right)\)
\(BC^2=AB^2+AC^2\Rightarrow AB^2=BC^2-AC^2=25^2-20^2=625-400=225=15^2\)
\(\Rightarrow AB=15\left(cm\right)\)
\(AH^2=HC.HB=16.9=4^2.3^2\Rightarrow AH=3.4=12\left(cm\right)\)
Bài 6:
\(AB=AC=4\left(cm\right)\) (Δ ABC cân tại A)
\(BH=HC=2\left(cm\right)\) (Ah là đường cao, đường trung tuyến cân Δ ABC)
\(BC=BH+HC=2+2=4\left(cm\right)\)
Chu vi Δ ABC :
\(4+4+4=12\left(cm\right)\)
HL
0
4D
1
MN
31 tháng 12 2021
NHỮNG ĐIỀU BỐ YÊU
Ngày con khóc tiếng chào đời
Bố thành vụng dại trước lời hát ru
Cứ “À ơi, gió mùa thu”
“Con ong làm mật”,
“Mù u! bướm vàng”…
Sau yêu cái chỗ con nằm
Thơm mùi sữa với chiếu thâm mấy quầngYêu sao ngang dọc, dọc ngang
Những hàng tã chéo mẹ giăng đầy nhà.
Thêm yêu dìu dịu nước hoa
Khi con muỗi đốt, bà xoa nhẹ nhàng
Và yêu một góc mặt bàn
Mèo con, chút chít xếp hàng đợi chơi.
Yêu ngày con gọi “Mẹ ơi”
Bước đi chập chững, Mặt Trời nhòm coi
Bao ngày, bao tháng dần trôi
Khắp nhà đầy ắp tiếng cười của con.
Để khi con vắng một hôm
Bố ngơ ngẩn nhớ, quên cơm bữa chiều.
Con ơi có biết bao điều
Sinh cùng con để bố yêu một đời.
PB
1
26 tháng 6 2016
áp dụng các hệ thức trong tam giác vuông ta có
\(AH^2=HB.HC\)
theo bài ra ta có
\(\frac{HB}{HC}=\frac{1}{4}\)=> \(\frac{HB}{1}=\frac{HC}{4}\) => \(\left(\frac{HB}{1}\right)^2=\left(\frac{HC}{4}\right)^2\) => \(\frac{HB^2}{1}=\frac{HC^2}{16}\)
áp dụng các tính chất của tỉ lệ thức ta có
\(\frac{HB^2}{1}=\frac{HC^2}{16}=\frac{HB.HC}{16}=\frac{AH^2}{16}=\frac{12^2}{16}=9\)
=> \(\frac{HB^2}{1}=9=>HB=3\)
=> \(\frac{HC^2}{16}=9=>HC=12\)
CH
Cô Hoàng Huyền
Admin
VIP
27 tháng 6 2016
Áp dung hệ thức lượng trong tam giác vuông, ta có: \(AH^2=BH.CH\Rightarrow AH^2=4BH^2\)
\(\Rightarrow BH=6\left(cm\right),CH=24\left(cm\right)\)
Chúc em học tốt :)
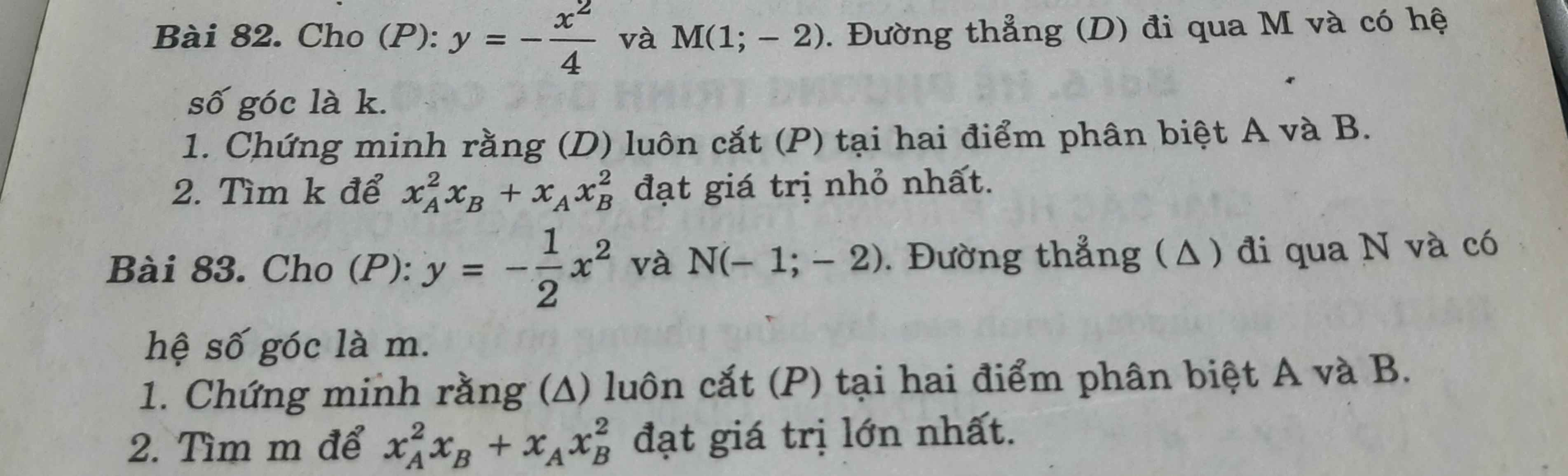
1 C
2 B
3 A
4 D
5 B
6 B
7 D
8 C
9 D
10 D
11 C
12 A
13 B
14 D
15 B