Trong Ví dụ 10, hãy tính các tích vô hướng \(\overrightarrow {AS} .\overrightarrow {BD} \) và \(\overrightarrow {AS} .\overrightarrow {CD} \).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
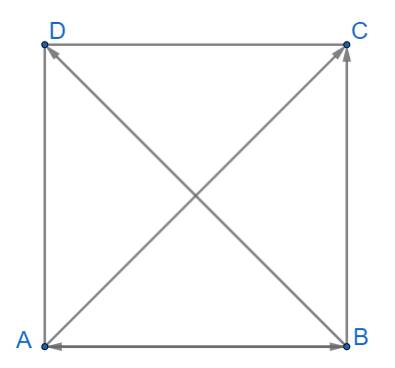
Ta có: \(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
+) \(AB \bot AD \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AD} \Rightarrow \overrightarrow {AB} .\overrightarrow {AD} = 0\)
+) \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = a.a\sqrt 2.\cos 45^\circ = a^2\)
+) \(\overrightarrow {AC} .\overrightarrow {CB} = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {CB} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = a\sqrt 2 .a.\cos 135^\circ = - {a^2}\)
+) \(AC \bot BD \Rightarrow \overrightarrow {AC} \bot \overrightarrow {BD} \Rightarrow \overrightarrow {AC} .\overrightarrow {BD} = 0\)
Chú ý
\(\overrightarrow {a} \bot \overrightarrow {b} \Leftrightarrow \overrightarrow {a} .\overrightarrow {b} = 0\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
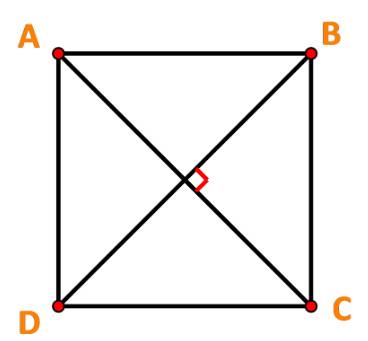
a) Ta có: \(AC = \sqrt {A{B^2} + A{D^2}} = \sqrt {2{a^2}} = a\sqrt 2 \)
\( \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = a.a\sqrt 2 .\cos \widehat {BAC} = {a^2}\sqrt 2 \cos {45^o} = {a^2}.\)
b) Dễ thấy: \(AC \bot BD \Rightarrow (\overrightarrow {AC} ,\overrightarrow {BD} ) = {90^o}\)
\( \Rightarrow \overrightarrow {AC} .\overrightarrow {BD} = AC.BD.\cos {90^o} = AC.BD.0 = 0.\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
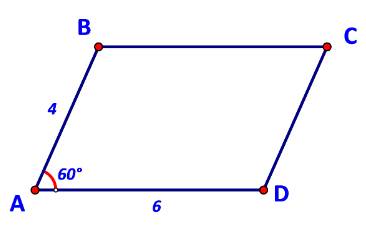
a) \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} ;\;\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .\)
b) \(\overrightarrow {AB} .\overrightarrow {AD} = 4.6.\cos \widehat {BAD} = 24.\cos {60^o} = 12.\)
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} = {4^2} + 12 = 28.\\\overrightarrow {BD} .\overrightarrow {AC} = (\overrightarrow {AD} - \overrightarrow {AB} )(\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AD} ^2} - {\overrightarrow {AB} ^2} = {6^2} - {4^2} = 20.\end{array}\)
c) Áp dụng định lí cosin cho tam giác ABD ta có:
\(\begin{array}{l}\quad \;B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\\ \Leftrightarrow B{D^2} = {4^2} + {6^2} - 2.4.6.\cos {60^o} = 28\\ \Leftrightarrow BD = 2\sqrt 7 .\end{array}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\(\begin{array}{l}\quad \;A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {4^2} + {6^2} - 2.4.6.\cos {120^o} = 76\\ \Leftrightarrow AC = 2\sqrt {19} .\end{array}\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 12 2020
\(\overrightarrow{AC}.\overrightarrow{BD}=\left(\overrightarrow{AD}+\overrightarrow{DC}\right)\left(\overrightarrow{BA}+\overrightarrow{AD}\right)\)
\(=\overrightarrow{AD}.\overrightarrow{BA}+\overrightarrow{AD}^2+\overrightarrow{DC}.\overrightarrow{BA}+\overrightarrow{DC}.\overrightarrow{AD}\)
\(=\overrightarrow{AD}^2-\overrightarrow{AB}.\overrightarrow{DC}=a^2-a.2a=-a^2\)
20 tháng 12 2022
a: AB=BC=CD=DA=6a
\(AC=BD=\sqrt{\left(6a\right)^2+\left(6a\right)^2}=6a\sqrt{2}\)
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=CB=6a\)
\(\left|\overrightarrow{BC}+\overrightarrow{BD}\right|=\sqrt{BC^2+BD^2+2\cdot BC\cdot BD\cdot cos45}\)
\(=\sqrt{36a^2+72a^2+\sqrt{2}\cdot6a\cdot6a\sqrt{2}}\)
\(=6a\sqrt{5}\)
b: \(\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\cdot AC\cdot cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=6a\cdot6a\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}\)
\(=36a^2\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
+) Ta có: \(AB \bot AC \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AC} \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0\)
+) \(\overrightarrow {AC} .\overrightarrow {BC} = \left| {\overrightarrow {AC} } \right|.\left| {\overline {BC} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right)\)
Ta có: \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt 2 \Leftrightarrow \sqrt {2A{C^2}} = \sqrt 2 \)\( \Rightarrow AC = 1\)
\( \Rightarrow \overrightarrow {AC} .\overrightarrow {BC} = 1.\sqrt 2 .\cos \left( {45^\circ } \right) = 1\)
+) \(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = 1.\sqrt 2 .\cos \left( {45^\circ } \right) = 1\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 1 2021
\(\overrightarrow{SA}.\overrightarrow{CD}=\overrightarrow{SA}.\overrightarrow{BA}=\overrightarrow{AS}.\overrightarrow{AB}=a.a.cos60^0=\dfrac{a^2}{2}\)
BT
19 tháng 5 2017
\(\left(\overrightarrow{a}+\overrightarrow{b}\right)^2=\left(\overrightarrow{a}+\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)\)\(=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2+2\overrightarrow{a}\overrightarrow{b}\).
\(\left(\overrightarrow{a}-\overrightarrow{b}\right)^2=\left(\overrightarrow{a}-\overrightarrow{b}\right)\left(\overrightarrow{a}-\overrightarrow{b}\right)\)\(=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2-2\overrightarrow{a}\overrightarrow{b}\).
\(\left(\overrightarrow{a}-\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)=\left|\overrightarrow{a}\right|^2+\overrightarrow{a}\overrightarrow{b}-\overrightarrow{a}\overrightarrow{b}+\left|\overrightarrow{b}\right|^2\)\(=\left|\overrightarrow{a}\right|^2-\left|\overrightarrow{b}\right|^2\).
Gọi O là giao điểm của hai đường chéo AC và BD trong hình vuông ABCD. Do đó, O là trung điểm của BD, O là trung điểm của AC.
Tứ giác ABCD là hình vuông cạnh a nên độ dài đường chéo BD là \(a\sqrt 2 \)\( \Rightarrow OB = \frac{{a\sqrt 2 }}{2}\)
Gọi E là trung điểm của SC. Mà O là trung điểm của AC nên OE là đường trung bình của tam giác SAC, do đó, OE//SA, \(OE = \frac{1}{2}SA = \frac{a}{2}\). Suy ra: \(\overrightarrow {AS} = 2\overrightarrow {OE} \)
Vì O là trung điểm của BD nên \(\overrightarrow {BD} = 2\overrightarrow {OB} \)
Vì tam giác SBC có ba cạnh bằng nhau nên tam giác SBC là tam giác đều. Do đó, BE là đường trung tuyến đồng thời là đường cao của tam giác SBC. Do đó, \(EB = \frac{{a\sqrt 3 }}{2}\).
Ta có: \(O{E^2} + O{B^2} = \frac{{{a^2}}}{4} + \frac{{{a^2}}}{2} = \frac{{3{a^2}}}{4} = E{B^2}\) nên \(\Delta \)EOB vuông tại O. Do đó, \(\overrightarrow {OE} \bot \overrightarrow {OB} \)
Ta có: \(\overrightarrow {AS} .\overrightarrow {BD} = 2\overrightarrow {OE} .\left( { - 2\overrightarrow {OB} } \right) = - 4\overrightarrow {OE} .\overrightarrow {OB} = 0\)
Tứ giác ABCD là hình vuông nên \(\overrightarrow {CD} = \overrightarrow {BA} \)
Ta có: \(\overrightarrow {AS} .\overrightarrow {CD} = \overrightarrow {AS} .\overrightarrow {BA} = - \overrightarrow {AS} .\overrightarrow {AB} = - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AB} } \right|\cos \left( {\overrightarrow {AS} ,\overrightarrow {AB} } \right) = - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AB} } \right|\cos \widehat {SAB}\)
Vì tam giác SAB có ba cạnh bằng nhau nên tam giác SAB đều, suy ra \(\widehat {SAB} = {60^0}\)
Suy ra: \(\overrightarrow {AS} .\overrightarrow {CD} = - \left| {\overrightarrow {AS} } \right|.\left| {\overrightarrow {AB} } \right|\cos \widehat {SAB} = - a.a.\cos {60^0} = \frac{{ - {a^2}}}{2}\)