Cho tam giác vuông tại A, đường cao AH, trưng tuyến AM.
a) So sanh góc BAH và MAC
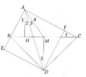
b) Trên đường trung trực Mx của đoạn thẳng BC, lấy điểm D sao cho MD = MA ( D, A ở hai nửa mặt phẳng khác nhau bờ BC). Chứng minh AD là phân giác chung của các góc MAH và CAB
c) Từ D kẻ DE, DF lần lượt vuông góc với AB, AC. Tứ giác AEDF là hình gì ?
d) Chứng minh tam giác DBE = tam giác DCF

a) Ta có: ^BAH = ^BCA (vì 2 góc này cùng phụ với ^B)
Mà: ^MAC = ^BCA (tg MAC cân tại M vì Tg ABC vuông tại A có AM là trung tuyến)
Nên: ^BAH = ^MAC (4)
b) Tg AMD cân tại M (vì MA=MD) => ^D = ^DAM (1)
Ta có: MD//AH ( vì MD_I_ HM, AH _I_ HM )
Nên: ^D = ^DAH (2)
(1)(2) => ^DAM = ^DAH (3) => AD là p/g của ^HAM (5)
(3)(4) => ^BAH + ^DAH = ^MAC + ^DAM <=> ^BAD=^CAD => AD là p/g của ^BAC (6)
(5)(6) => AD là p/g chung của ^HAM và ^BAC
c) Ta có: AEDF là hcn ( vì ^E=^F=^A=90o )
Mà: AD là p/g của ^EAC (cmt)
Nên: AEDF là hình vuông
d) Tg DBE (^DEA=90o) và tg DCF (^DFC=90o) có:
DE = DF (AEDF là hình vuông)
DB = DC (MD là đường trung trực của BC)
Nên: Tg DBE = tg DCF (ch-cgv)
bạn vẽ hình kiểu j thế?????