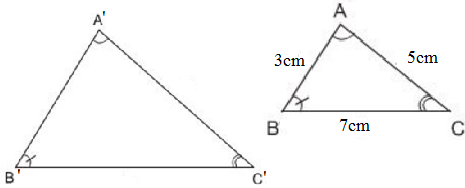
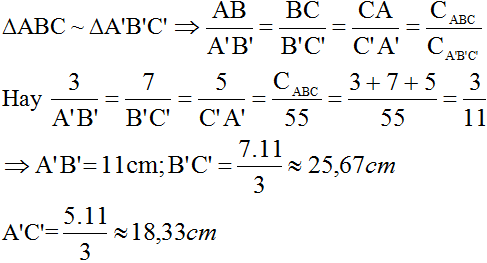Tam giác thứ nhất có độ dài các cạnh là 2,6cm,7,1cm,8cm tam giác thứ hai có các cạnh là 78,21,3,24cm hỏi hai tam giác đó có đồng dạng ko vì sao
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 11 2017
Chu vi tam giác ABC là: AB + BC + CA = 3 + 7 + 5 = 15 (cm)
Δ A’B’C’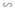 
ΔABC ⇒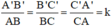 
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
31 tháng 1 2023
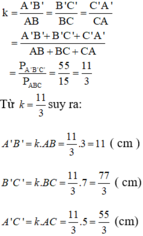
Tổng ba cạnh tam giác lúc đầu là : 327,46 cm
Khi tăng cạnh thứ nhất thêm 2,46cm và giảm cạnh thứ hai đi 5,32cm thì tổng ba cạnh của tam giác lúc sau là:
327, 46 + 2,46 - 5,32 = 324,6 (cm)
Mỗi cạnh của tam giác lúc sau bằng nhau và bằng :
324,6 : 3 = 108,2 (cm)
Vì cạnh thứ nhất tăng thêm và cạnh thứ hai giảm đi thì ba cạnh bằng nhau nên cạnh thứ nhất là cạnh bé nhất và có độ dài là:
108,2 - 2,46 = 105,74 (cm)
Cạnh hình vuông cạnh cạnh bé nhất của tam giác và bằng 105,74 cm
Diện tích hình vuông là:
105,74 x 105,74 = 11180,9476 (cm2)
Đs....
22 tháng 4 2017
∆ABC ∽ ∆A'B'C' => = = =
hay = = = =
=> A'B' = 11cm;
B'C' = ≈ 25.67 cm
A'C' = ≈ 18,33 cm
H9
HT.Phong (9A5)
CTVHS
22 tháng 3 2023
Độ dài của cạnh thứ 1 là: \(\dfrac{7}{10}cm=\dfrac{7}{100}dm\)
Độ dài cạnh thứ 3 là: \(\dfrac{3}{4}+\dfrac{3}{20}=\dfrac{15}{20}+\dfrac{3}{20}=\dfrac{18}{20}=\dfrac{9}{10}dm\)
Chu vi tam giác đó: \(\dfrac{7}{100}+\dfrac{3}{4}+\dfrac{9}{10}=\dfrac{7}{100}+\dfrac{75}{100}+\dfrac{90}{100}=\dfrac{172}{100}=\dfrac{43}{25}\left(dm\right)\)
AF
27 tháng 2 2018
ta có 316 : 4 = 79
=> cạnh thứ nhất là 79m và cạnh thứ 2 là 79.3 là 237m
S mảnh đất là: 1/2 . 79 . 237 = 9361,5 m
27 tháng 2 2018
Cạnh góc vuông thứ nhất : 3 phần
Cạnh góc vuông thứ hai : 1 phần
Tổng = 316 m
Cạnh góc vuông thứ nhất dài là
316:(1+3)x3=237(m)
Cạnh góc vuông thứ hai dài là
316-237=79(m)
Diện tích mảnh đất hình tam giác là
237x79:2=9361,5(m2)
Đáp số : 9361,5 m2
29 tháng 12 2016
Hai lần chu vi tam giác ABC là : 18,25 + 23,55 + 20,3 = 62,1 ( cm )
Giải thích : Cạnh 1 + Cạnh 2 + Cạnh 2 + Cạnh 3 + Cạnh 1 + Cạnh 3 = 62,1 nên 62,1 là 2 lần chu vi
Chu vi tam giác ABC là : 62,1 : 2 = 31,05 ( cm )
Đáp số : 31,05 cm.
OK,k mik nha
4 tháng 3 2018
Chu vi tam giác ABC là 3 + 5 +7 = 15
Ta có :
P ABC / P A'B'C' = AB / A'B'
<=> 15 / 55 = 3 / A'B'
=> A'B' = ( 55 x 3 )/ 15 = 11 cm
P ABC / P A'B'C' = AC / A'C'
<=> 15 / 55 = 5 / A'C'
=> A'C' = ( 55 x 5 ) / 15 = 55/3 cm
P ABC / P A'B'C' = BC / B'C'
<=> 15 / 55 = 7 / B'C'
=> B'C' = ( 55 x 7 ) / 15 = 77/3 cm
HH
17 tháng 4 2020
\(\Rightarrow\Delta ABC\)đồng dạng \(\Delta A'B'C'\left(gt\right)\)
Áp dụng tính chất DTSBN , ta có :
\(\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}=\frac{AB+AC+BC}{A'B'+A'C'+B'C'}=\frac{C_{ABC}}{C_{A'B'C'}}\)
Hay \(\frac{3}{A'B'}=\frac{7}{B'C'}=\frac{5}{A'C'}=\frac{C_{ABC}}{55}=\frac{3+5+7}{55}=\frac{15}{55}=\frac{3}{11}\)
Với CABC và CA'B'C' lần lượt là chu vi của tam giác ABC , A'B'C'
\(+)\frac{3}{A'B'}=\frac{3}{11}\Rightarrow A'B'=\frac{3.11}{3}=11cm\)
\(+)\frac{7}{A'C'}=\frac{3}{11}\Rightarrow B'C'=\frac{7.11}{3}\approx25,67cm\)
\(+)\frac{5}{A'C'}=\frac{3}{11}\Rightarrow A'C'=\frac{5.11}{3}\approx18,33cm\)