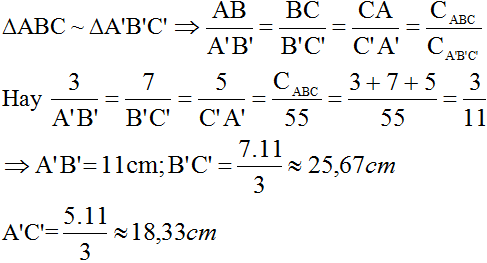Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

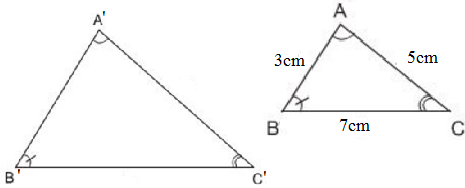
Chu vi tam giác ABC là: AB + BC + CA = 3 + 7 + 5 = 15 (cm)
Δ A’B’C’ 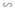 ΔABC ⇒
ΔABC ⇒ 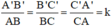
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
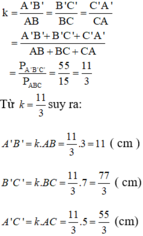

∆ABC ∽ ∆A'B'C' => ABA′B′ABA′B′ = BCB′C′BCB′C′= CAC′A′CAC′A′ = CABCCA′B′C′CABCCA′B′C′
hay 3A′B′3A′B′ = 7B′C′7B′C′ = 5A′C′5A′C′ = CABC55CABC55 = 311311
=> A'B' = 11cm;
B'C' = 7.1137.113 ≈ 25.67 cm
A'C' = 5.1135.113 ≈ 18,33 cm

Chu vi tam giác ABC là 3 + 5 +7 = 15
Ta có :
P ABC / P A'B'C' = AB / A'B'
<=> 15 / 55 = 3 / A'B'
=> A'B' = ( 55 x 3 )/ 15 = 11 cm
P ABC / P A'B'C' = AC / A'C'
<=> 15 / 55 = 5 / A'C'
=> A'C' = ( 55 x 5 ) / 15 = 55/3 cm
P ABC / P A'B'C' = BC / B'C'
<=> 15 / 55 = 7 / B'C'
=> B'C' = ( 55 x 7 ) / 15 = 77/3 cm
A B C A' B' C'
\(\Rightarrow\Delta ABC\)đồng dạng \(\Delta A'B'C'\left(gt\right)\)
Áp dụng tính chất DTSBN , ta có :
\(\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}=\frac{AB+AC+BC}{A'B'+A'C'+B'C'}=\frac{C_{ABC}}{C_{A'B'C'}}\)
Hay \(\frac{3}{A'B'}=\frac{7}{B'C'}=\frac{5}{A'C'}=\frac{C_{ABC}}{55}=\frac{3+5+7}{55}=\frac{15}{55}=\frac{3}{11}\)
Với CABC và CA'B'C' lần lượt là chu vi của tam giác ABC , A'B'C'
\(+)\frac{3}{A'B'}=\frac{3}{11}\Rightarrow A'B'=\frac{3.11}{3}=11cm\)
\(+)\frac{7}{A'C'}=\frac{3}{11}\Rightarrow B'C'=\frac{7.11}{3}\approx25,67cm\)
\(+)\frac{5}{A'C'}=\frac{3}{11}\Rightarrow A'C'=\frac{5.11}{3}\approx18,33cm\)

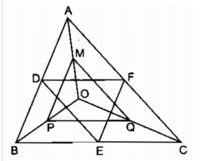
Theo giả thiết D, E, F lần lượt là trung điểm các cạnh AB, BC và CA nên DE, EF, FD là các đường trung bình của tam giác ABC. Do đó, ta có:
DE = 1/2 AC,EF = 1/2 AB,FD = 1/2 BC (1)
Mặt khác, M là trung điểm của OA, P là trung điểm của OB, Q là trung điểm của OC, xét các tam giác OAB, OBC, OCA, ta cũng có:
MP = 1/2 AB,PQ = 1/2 BC, QM = 1/2 AC. (2)
Từ đẳng thức (1) và (2), ta suy ra :
DE = QM, EF = MP, FD = PQ.
Do đó ta có: 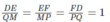
Vậy △ DEF đồng dạng △ QMP theo tỉ số đồng dạng k = 1, trong đó D, E, F lần lượt tương ứng với các đỉnh Q, M, P.

a: Ta có: ΔA'B'C'∼ΔABC
nên A'B'/AB=B'C'/BC=A'C'/AC
=>A'B'/6=B'C'/12=A'C'/8=3/2
=>A'B'=9cm; B'C'=18cm; A'C'=12cm
b: Ta có: ΔA'B'C'∼ΔABC
nên \(\dfrac{C_{A'B'C'}}{C_{ABC}}=\dfrac{3}{2}\)