vẽ hình luôn ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 4 2022
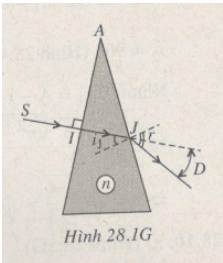
Câu 9.
Tại điểm \(I\): \(i=r=0\)
Tia sáng truyền thẳng vào lăng kính.
Tại điểm J có \(i_J=30^o\)
Theo định luật khúc xạ ánh sáng:
\(sinr=nsini_J=1,5\cdot sin30^o=\dfrac{3}{4}\Rightarrow r=arcsin\dfrac{3}{4}\)
Góc lệch:
\(D=r-i_J=arcsin\dfrac{3}{4}-30^o\approx18,6^o\)
Chọn B.
Hình vẽ tham khảo sgk lí 11!!!
20 tháng 12 2021
a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{O}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=CB
23 tháng 2 2022
a: Xét ΔCAD vuông tại A và ΔCED vuông tại E có
CD chung
CA=CE
Do đó:ΔCAD=ΔCED
Suy ra: DA=DE
b: Xét ΔADK vuông tại A và ΔEDB vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDB}\)
Do đó:ΔADK=ΔEDB
c: AB=8cm
vẽ hình luôn giúp em ạ
22 tháng 4 2023
3:
a: AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔDCB có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>CM=2/3*8=16/3cm
c: Gọi H là trung điểm của AC
=>HQ//AD(HQ vuông góc AC)
mà H là trung điểm của AC
nên Q là trung điểm của CD
=>B,M,Q thẳng hàng
10 tháng 12 2023
1:
a: Xét ΔOBA và ΔOCA có
OB=OC
AB=AC
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OBA}=\widehat{OCA}\)
mà \(\widehat{OBA}=90^0\)
nên \(\widehat{OCA}=90^0\)
=>AC\(\perp\)OC tại C
=>AC là tiếp tuyến của (O)
b: Xét (O) có
ΔBCE nội tiếp
BE là đường kính
Do đó: ΔBCE vuông tại C
=>BC\(\perp\)CE tại C
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC
Ta có: OA\(\perp\)BC
CE\(\perp\)CB
Do đó: OA//CE
2: Gọi giao điểm của EC với BA là K
Ta có: BC\(\perp\)CE tại C
=>BC\(\perp\)EK tại C
=>ΔBCK vuông tại C
Ta có: \(\widehat{ACK}+\widehat{ACB}=\widehat{BCK}=90^0\)
\(\widehat{AKC}+\widehat{ABC}=90^0\)(ΔBCK vuông tại C)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ACK}=\widehat{AKC}\)
=>AC=AK
mà AC=AB
nên AK=AB(3)
Ta có: CH\(\perp\)BE
BA\(\perp\)BE
Do đó: CH//BA
Xét ΔEBA có MH//BA
nên \(\dfrac{MH}{BA}=\dfrac{EM}{EA}\left(4\right)\)
Xét ΔEAK có MC//AK
nên \(\dfrac{MC}{AK}=\dfrac{EM}{EA}\left(5\right)\)
Từ (3),(4),(5) suy ra MH=MC
=>M là trung điểm của CH
VH
1
5 tháng 4 2022
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
Do đó: ΔHBA\(\sim\)ΔABC
b: \(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=3.6\left(cm\right)\)
CH=BC-BH=6,4(cm)
20 tháng 11 2023
\(M\in SA\subset\left(SAB\right)\)
\(M\in\left(P\right)\)
Do đó: \(M\in\left(SAB\right)\cap\left(P\right)\)
Xét (SAB) và (P) có
\(M\in\left(SAB\right)\cap\left(P\right)\)
AB//CD
Do đó: \(\left(SAB\right)\cap\left(P\right)=xy\), xy đi qua M và xy//AB//CD
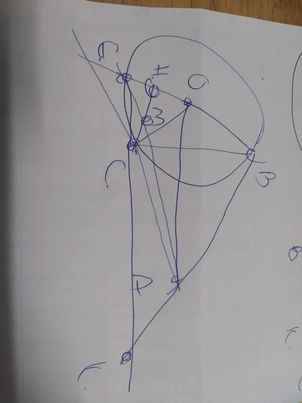
1: Ta có: ΔOCD cân tại O
mà OI là đường cao
nên I là trung điểm của CD
Xét tứ giác OCAD có
I là trung điểm chung của OA và CD
=>OCAD là hình bình hành
Hình bình hành OCAD có OC=OD
nên OCAD là hình thoi
2: Ta có: OCAD là hình thoi
=>OA là phân giác của góc COD
Xét ΔOCM và ΔODM có
OC=OD
\(\widehat{COM}=\widehat{DOM}\)
OM chung
Do đó: ΔOCM=ΔODM
=>\(\widehat{OCM}=\widehat{ODM}\)
mà \(\widehat{OCM}=90^0\)
nên \(\widehat{ODM}=90^0\)
=>MD là tiếp tuyến của (O)
3:
Xét (O) có
ΔCFE nội tiếp
CE là đường kính
Do đó: ΔCFE vuông tại F
=>CF\(\perp\)FE tại F
=>CF\(\perp\)ME tại F
Xét ΔCME vuông tại C có CF là đường cao
nên \(MF\cdot ME=MC^2\left(1\right)\)
Xét ΔMCO vuông tại C có CI là đường cao
nên \(MI\cdot MO=MC^2\left(2\right)\)
Từ (1) và (2) suy ra \(MF\cdot ME=MI\cdot MO\)
=>\(\dfrac{MF}{MO}=\dfrac{MI}{ME}\)
Xét ΔMFI và ΔMOE có
\(\dfrac{MF}{MO}=\dfrac{MI}{ME}\)
\(\widehat{FMI}\) chung
Do đó: ΔMFI đồng dạng với ΔMOE