
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



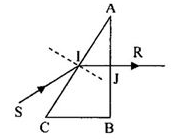
Theo đinh luật khúc xạ ánh sáng (tại điểm \(I\)) :
\(sini_1=nsinr_1\)
\(\Rightarrow sin45^o=\sqrt{2}\cdot sinr_1\Rightarrow sinr_1=\dfrac{1}{2}\Rightarrow r_1=30^o\)
Tam giác ABC đều\(\Rightarrow\)Góc chiết quang \(\widehat{A}=60^o=r_1+r_2\)
\(\Rightarrow r_2=30^o\)
Xét tại điểm J, theo định luật khúc xạ ánh sáng:
\(sini_2=nsinr_2=\sqrt{2}\cdot sin30^o=\dfrac{\sqrt{2}}{2}\Rightarrow i_2=45^o\)
Góc lệch tia ló ra khỏi lăng kính so với tia tới:
\(D=i_1+i_2-A=45^o+45^o-60^o=30^o\)
Chọn A

Góc giới hạn phản xạ toàn phần:
\(sini_{gh}=\dfrac{n_2}{n_1}\)
\(\Rightarrow sini_{gh}=\dfrac{\dfrac{4}{3}}{\sqrt{3}}=\dfrac{4\sqrt{3}}{9}\)
\(\Rightarrow i_{gh}=50,2^o\)
Chọn A

Câu 12.
Ta có: \(\dfrac{sini}{sinr}=n\Rightarrow\dfrac{sin60^o}{sinr}=1,5\)
\(\Rightarrow sinr=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow r\approx35,3^o\)
Chọn C

Câu 17.
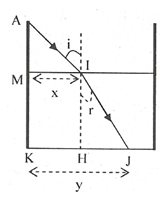
Xét tam giác IHJ vuông tại H:
\(sinr=\dfrac{HJ}{IJ}=\dfrac{HJ}{\sqrt{HI^2+HJ^2}}\)
Chiết xuất: \(\dfrac{sini}{sinr}=n\)
\(\Rightarrow\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{HI^2+HJ^2}}{HJ}=\dfrac{4}{3}\)
\(\Rightarrow\dfrac{3}{4}\cdot\dfrac{60^2+HJ^2}{HJ^2}=\dfrac{16}{9}\Rightarrow HJ=51,25cm\)
Độ dài bóng của thành bể tạo ở đáy:
\(HJ+x=85,9cm\)
Chọn A

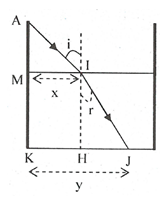
Xét \(\Delta HIJ\) vuông tại H:
\(sinr=\dfrac{HJ}{IJ}=\dfrac{HJ}{\sqrt{HI^2+HJ^2}}\)
\(\Rightarrow\dfrac{sini}{sinr}=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{HI^2+HJ^2}}{HJ}=n\)
\(\Rightarrow\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{60^2+HJ^2}}{HJ}=\dfrac{4}{3}\)
\(\Rightarrow HJ=51,25cm\)
Độ dài vệt sáng:
\(y=x+HJ=85,9cm\)
Chọn B











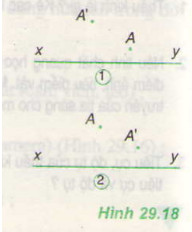

Câu 9.
Tại điểm \(I\): \(i=r=0\)
Tia sáng truyền thẳng vào lăng kính.
Tại điểm J có \(i_J=30^o\)
Theo định luật khúc xạ ánh sáng:
\(sinr=nsini_J=1,5\cdot sin30^o=\dfrac{3}{4}\Rightarrow r=arcsin\dfrac{3}{4}\)
Góc lệch:
\(D=r-i_J=arcsin\dfrac{3}{4}-30^o\approx18,6^o\)
Chọn B.
Hình vẽ tham khảo sgk lí 11!!!