Tìm \(n\in N\)để :\(n^2+2n+6⋮n+1\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
23 tháng 12 2019
a, n+6 ⋮ n+2 => (n+2)+4 ⋮ n+2
=> 4 ⋮ n+2
=> n ∈ {0;2}
b, 2n+3 ⋮ n - 2
=> 2.(n - 2)+7 ⋮ n - 2
=> 7 ⋮ n - 2
=> n ∈ {3;9}
c, 3n - 1 ⋮ 3 - 2n
=> 2.(3n - 1) ⋮ 3 - 2n
=> 6n - 2 ⋮ 3 - 2n
Ta có: 3(3 - 2n) ⋮ 3 - 2n => 9 - 6n ⋮ 3 - 2n
Do đó: (6n - 2)+(9 - 6n) ⋮ 3 - 2n
=> 7 ⋮ 3 - 2n => n ∈ {1}
LD
4
3 tháng 3 2020
a) => n-1+3 chia hết n-1
Mà n-1 chia hết n-1
=> 3 chia hết cho n-1
=> n-1 thuộc Ước của 3
........
b)=> 2(n+1) +5 chia hết n+1
mà 2(n+1) chia hết n+1
=> 5 chia hết cho n+1
=> n+1 thuộc ước của 5
.......
3 tháng 3 2020
a,Ta có :\(n+2⋮n-1\)
\(=>n-1+3⋮n-1\)
Do \(n-1⋮n-1\)
\(=>3⋮n-1\)
\(=>n-1\inƯ\left(3\right)\)
\(=>n-1\in\left\{-3;-1;1;3\right\}\)
\(=>n\in\left\{-2;0;2;4\right\}\)
b,\(2n+7⋮n+1\)
\(=>2.\left(n+1\right)+5⋮n+1\)
Do \(2.\left(n+1\right)⋮n+1\)
\(=>5⋮n+1\)
\(=>n+1\inƯ\left(5\right)\)
\(=>n+1\in\left\{-5;-1;1;5\right\}\)
\(=>n\in\left\{-6;-2;0;4\right\}\)
MC
3
3 tháng 3 2020
Ta có: \(n^2+1=\left(n-1\right)^2+2n\)
Để \(n^2+1\)chia hết cho n-1 thì 2n phải chia hết cho n-1
Ta có 2n=2(n-1)+2
Mà n thuộc N => n-1 thuộc N
=> n-1 thuộc Ư (2)={1;2}
Nếu n-1=1 => n=2
Nếu n-1=2 => n=3
U
20 tháng 2 2018
\(b,n+4⋮n+2\)
\(\Rightarrow n+2+2⋮n+2\)
\(n+2⋮n+2\)
\(\Rightarrow2⋮n+2\)
\(\Rightarrow n+2\inƯ\left(2\right)=\left\{1;2\right\}\)
\(\Rightarrow n\in\left\{-1;0\right\}\) mà n thuộc N
=> n = 0
d, \(2n+6⋮n+3\)
\(\Rightarrow2\left(n+3\right)⋮n+3\)
\(n+3⋮n+3\Rightarrow2\left(n+3\right)⋮n+3\)
\(\Rightarrow\) n = bao nhiêu cx đc miễn là n thuộc N
LD
2
TH
3 tháng 3 2020
2n + 1 ⋮ 6 - n
=> 2n + 1 ⋮ n - 6
=> 2n - 12 + 13 ⋮ n - 6
=> 2(n - 6) + 13 ⋮ n - 6
=> 13 ⋮ n - 6
=> n - 6 thuộc Ư(13)
=> n - 6 thuộc {-1; 1; - 13; 13}
=> n thuộc {5; 7; -7; 19}
HT
3 tháng 3 2020
\(2n+1⋮6-n\)
\(\Rightarrow2\left(6-n\right)+12+1⋮6-n\)
\(\Rightarrow2\left(6-n\right)+13⋮6-n\)
\(\Rightarrow13⋮6-n\)
\(\Rightarrow6-n\inƯ\left(13\right)=\left\{1;13\right\}\)
\(\text{Khi 6-n=1}\)\(\Rightarrow n=5\left(\text{Nhận}\right)\)
\(\text{Khi 6-n=13}\)\(\Rightarrow n=-7\left(\text{Loại}\right)\)
ND
0
23 tháng 2 2019
Để A thuộc luôn tồn tại mà n thuộc Z suy ra n+8 chia hết cho 2n-5
suy ra (n+8).2 chia hết cho n+8 hay2n+16
Suy ra (2n+16)-(2n-5) chian hết cho 2n-5
suy ra 21 chia hết cho 2n-5suy ra 2n-5 thuộc Ư(21)={-21;;21;3;-3;7;-7;1;-1}
suy ra 2n thuộc{-16;26;8;2;12;-2;6;4}
suy ra n thuộc{-8;13;4;1;6;-1;3;2}
Vậy n thuộc{-8;13;4;1;6;-1;3;2}
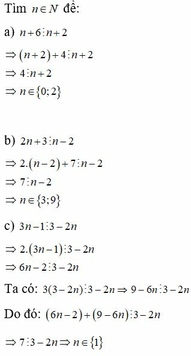
n2+2n+6=n2+2n+1+5=(n+1)2+5 chia hết cho n+1
mà (n+1)2 chia hết cho n+1 => 5 chia hết cho n+1 <=> n+1 thuộc Ư(5}={-5;-1;1;5} <=> n thuộc {-6;-2;0;4}
mà n thuộc N nên n=0 hoặc n=4