Bài 1: Cho (O) và (O') tiếp xúc ngoài tại A . Vẽ một đường thẳng qua A cắt (O) tại C và cắt (O') tại D . Vẽ các đường kính CE và DF
a) C/m góc OCA = O'DA
b) C/m OC//OD
c) C/m AC vuông góc AE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 3 2021
bài 1. Góc KOM có độ là:
(80-20)/2=30 (độ)
Góc MOH có độ là:
30+20=50 (độ)
Vậy góc MOH=50 độ
KOM=30 độ
T
9 tháng 5 2021
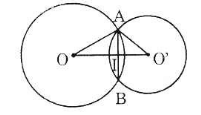
- Trường hợp 1: O và O' nằm khác phía đối với AB
Gọi I là giao điểm của OO' và AB. Theo tính chất đường nối tâm ta có:
AB ⊥ OO' và AI = IB = 12
Áp dụng định lí Pitago, ta được:
Vậy OO' = OI + IO' = 16 + 9 = 25 (cm)
- Trường hợp 2: O và O' nằm cùng phía đối với AB
Tương tự như trường hợp 1, ta có:
Vậy OO' = OI – O'I = 16 – 9 = 7 (cm).
17 tháng 11 2023
a: Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
b: Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
mà OA=OB
nên OM là đường trung trực của AB
=>OM\(\perp\)AB tại H và H là trung điểm của AB
c: Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OH\cdot OM=R^2\)
PH
2
13 tháng 9 2021
Lời giải:
Gọi dây trên là dây AB. Hạ OH⊥⊥AB = {H} (cd)
Xét (O) 1 phần đường kính OH: OH⊥⊥AB = {H} (cd)
=> H là trung điểm AB (đl) => HA = HB = AB: 2 = 12:2 = 6 (cm)
OH⊥⊥AB = {H} (cd) => ΔΔOHB vuông tại H (đn)
=> OH22+ HB22= OB22(Đl Py-ta-go)
T/s: OH22+ 622= R22
<=> OH22+36 = 1022=100
<=> OH22= 64 => OH = 8 (cm)
13 tháng 9 2021
Gọi H là chân đường cao kẻ từ O
=> H là trung điểm AB
=> AH = AB/2 = 12/2 = 6 cm
Theo định lí Pytago cho tam giác AOH vuông tại H
\(AO^2=OH^2+AH^2\Rightarrow OH^2=AO^2-AH^2=100-36=64\Rightarrow OH=8\)cm
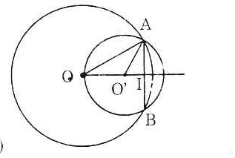
a) Đặt R là bán kính đường tròn tâm O
r là bán kính đường tròn tâm O'
Ta có:
OC = OA = R
∆OAC cân tại O
⇒ ∠OAC = ∠OCA
Mà ∠OAC = ∠O'AD (đối đỉnh)
⇒ ∠OCA = ∠O'AD (1)
Lại có:
O'A = OD = r
⇒ ∆O'AD cân tại O'
⇒ ∠O'AD = ∠O'DA (2)
Từ (1) và (2) suy ra ∠OCA = ∠O'DA
b) Sửa đề: chứng minh OC // O'D
Do ∠OCA = ∠O'DA (cmt)
Mà ∠OCA và ∠O'DA là hai góc so le trong
⇒ OC // O'D
c) Do CE là đường kính của đường tròn tâm O
A nằm trên đường tròn tâm O
⇒ ∆ACE vuông tại A
Hay AC ⊥ AE