Cho E là một biến cố và \(\Omega \) là không gian mẫu. Tính n(\(\overline E \)) theo n(\(\Omega \)) và n(E).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
Không thể tính n(\(\Omega \)), n(F) và n(G) bằng cách liệt kê ra hết các phần tử của \(\Omega \), F và G rồi kiểm đếm.
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
a) Không gian mẫu \(\Omega = \left\{ {1;2;3;4;5;6;7;8;9;10;11;12} \right\}\). Các kết quả xảy ra có đồng khả năng với nhau.
b) Biến cố \(E = \left\{ {2;3;5;7;11} \right\}\).
c) Phép thử có 12 kết quả có thể xảy ra. Biến cố E có 5 kết quả có lợi.
Vậy xác suất của biến cố E là \(\frac{5}{{12}}\).
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
a) Ta có \(\Omega = \left\{ {1;2;...;22} \right\}\).
b) \(B = \left\{ {3;6;9;12;15;18;21} \right\}\).
\(\overline A = \left\{ {1;2;4;5;7;8;10;11;13;14;16;17;19;20;22} \right\}\).
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
a) Ta có \(\Omega = \left\{ {1;2;...;30} \right\}\).
b) \(A = \left\{ {2;3;5;7;11;13;17;19;23;29} \right\}\).
\(\overline A = \left\{ {1;4;6;8;9;10;12;14;15;16;18;20;21;22;24;25;26;27;28;30} \right\}\).
1 tháng 8 2020
Chị ơi em chưa hiểu đoạn P=U2*RN/(Rn+r)2 có phải = I2*Rn
Mà I2 không phải là E2/(Rn+n)2 hoặc U2/Rn2
Chị giải thích giúp em với ạ, em cảm ơn!
19 tháng 3 2016
Gọi \(\overrightarrow{u},\overrightarrow{v}\) theo thứ tự là vec tơ chỉ phương đơn vị của các tia Ox, Oy, tương ứng cùng hướng với các tia Ox, Oy gọi I là tâm của \(\omega\). Chọn O làm gốc vec tơ điểm và với mỗi điểm X của mặt phẳng, ký hiệu \(\overrightarrow{x}\) để chỉ vec tơ \(\overrightarrow{OX}\). Trung trực OA cắt các đường thẳng \(d_1,d_2\) theo thứ tự tại B, C.
Khi đó B, C cố định và do I nằm trên đường thẳng BC nên \(\overrightarrow{i}=\alpha\overrightarrow{b}+\left(1-\alpha\right)\overrightarrow{c}\)
Mặt khác , theo định lí chiếu ta có :
\(\overrightarrow{m}=2\left(\overrightarrow{i}.\overrightarrow{u}\right).\overrightarrow{u}\) và \(\overrightarrow{n}=2\left(\overrightarrow{i}.\overrightarrow{v}\right).\overrightarrow{v}\)
Gọi P là trung điểm MN. Suy ra \(2\overrightarrow{p}=\overrightarrow{m}.\overrightarrow{n}\). Bởi vậy, với \(b=OB,c=OC\) và \(t=\cos<\left(\overrightarrow{u}\overrightarrow{v}\right)\) thì b, c, t là các hằng số và :
\(\overrightarrow{p}=\left[\alpha.\overrightarrow{b}\overrightarrow{u}+\left(1-\alpha\right).\overrightarrow{c}.\overrightarrow{u}\right].\overrightarrow{u}+\left[\alpha.\overrightarrow{b}\overrightarrow{v}+\left(1-\alpha\right).\overrightarrow{c}.\overrightarrow{v}\right].\overrightarrow{v}\)
\(=\alpha.b\left(\overrightarrow{u}+t\overrightarrow{v}\right)+\left(1-\alpha\right).c\left(t\overrightarrow{u}+\overrightarrow{v}\right)\)
\(=\alpha\overrightarrow{x}+\left(1-\alpha\right)\overrightarrow{y}\)
Trong đó \(\overrightarrow{x}=\overrightarrow{OX}=b\left(\overrightarrow{u}+t\overrightarrow{v}\right)\) và \(\overrightarrow{y}=\overrightarrow{OY}=c\left(t\overrightarrow{u}+\overrightarrow{v}\right)\) là các vec tơ cố định
Suy ra P luôn nằm trên đường thẳng XY cố định khi \(\omega\) thay đổi
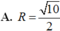
Ta có \(n\left( {\overline E } \right) = n\left( \Omega \right) - n\left( E \right)\).