4x.8x=1024
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 10 2021
ta có 4 x 3 y 2 – 8 x 2 y 3 = 4 x 2 y 2 . x – 4 x 2 y 2 . 2 y = 4 x 2 y 2 ( x – 2 y )
Vậy 4x3y2 – 8x2y3 = 4x2y2(x – 2y)
Đáp án cần chọn là: C
bấm đúng cho mik đi
CM
10 tháng 12 2019
Đáp án D
Lời giải:
Đặt t = x − 512 1024 − x 8 ≥ 0 , ta có
t 4 = x − 512 1024 − x ≤ x − 512 + 1024 − x 2 = 256 ⇒ 0 ≤ t ≤ 4
Với t = 4 thì ta tìm được 1 giá trị của x = 768
Với 0 ≤ t ≤ 4 thì ta tìm được 2 giá trị của x (Khi đó phương trình của Định lý Viét đảo có 2 nghiệm phân biệt)
Bình phương 2 vế phương trình đã cho, ta được
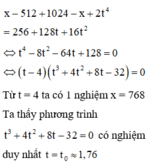
(sử dụng máy tính).
Từ đó ta có 2 nghiệm x thỏa mãn
Do đó phương trình đã cho có 3 nghiệm.
CM
11 tháng 7 2017
Đáp án C
x - 512 + 1024 - x = 16 + 4 x - 512 1024 - x 8 (*), 512 ≤ x ≤ 1024
t = x - 512 1024 - x 8 ⇒ t 4 = x - 512 1024 - x ≤ x - 512 + 1024 - x 2 = 256 ⇒ 0 ≤ t ≤ 4 t = 4 ⇒ x = 768 0 ≤ t ≤ 4
=> Bình phương hai vế (*):
( t - 4 ) t 3 + 4 t 2 + 8 t - 32 = 0 ⇔ [ x ≈ 512 , 18 x ≈ 1023 , 82
CM
20 tháng 4 2019
Đáp án C
x − 512 + 1024 − x = 16 + 4 ( x − 512 ) ( 1024 − x ) 8 ( * ) , ( 512 ≤ x ≤ 1024 ) t = ( x − 512 ) ( 1024 − x ) 8 ⇒ t 4 = ( x − 512 ) ( 1024 − x ) ≤ x − 512 + 1024 − x 2 = 256 ⇒ 0 ≤ t ≤ 4 ⋅ t = 4 ⇒ x = 768
0 ≤ t < 4 ⇒ bình phương 2 vế (*):
⇒ ( t − 4 ) ( t 3 + 4 t 2 + 8 t − 32 ) = 0 ⇔ t ≈ 1 , 76 ⇔ x ≈ 512 , 18 x ≈ 1023 , 82
KT
2
TB
26 tháng 5 2021
\(\dfrac{x-1}{2x^2-4x}-\dfrac{7}{8x}=\dfrac{5-x}{4x^2-8x}-\dfrac{1}{8x-16}\) ( ĐKXĐ: \(x\ne0;x\ne2\) )
\(\Leftrightarrow\dfrac{x-1}{2x\left(x-2\right)}-\dfrac{7}{8x}=\dfrac{5-x}{4x\left(x-2\right)}-\dfrac{1}{8\left(x-2\right)}\)
\(\Leftrightarrow\dfrac{\left(x-1\right)4}{8x\left(x-2\right)}-\dfrac{7\left(x-2\right)}{8x\left(x-2\right)}=\dfrac{2\left(5-x\right)}{8x\left(x-2\right)}-\dfrac{1x}{8x\left(x-2\right)}\)
\(\Rightarrow4x-4-7x+14=10-2x-x\)
\(\Leftrightarrow-3x+2x+x=10+4-14\)
\(\Leftrightarrow0=0\)
Vậy pt đã cho có nghiệm đúng với mọi x
NT
1
QA
19 tháng 3 2021
Trả lời:
\(\frac{x-1}{2x^2-4x}-\frac{7}{8x}=\frac{5-x}{4x^2-8x}-\frac{1}{8x-16}\)\(\left(đkxđ:x\ne0;x\ne2\right)\)
\(\Leftrightarrow\frac{x-1}{2x\left(x-2\right)}-\frac{7}{8x}=\frac{5-x}{4x\left(x-2\right)}-\frac{1}{8\left(x-2\right)}\)
\(\Leftrightarrow\frac{4\left(x-1\right)}{8x\left(x-2\right)}-\frac{7\left(x-2\right)}{8x\left(x-2\right)}=\frac{2\left(5-x\right)}{8x\left(x-2\right)}-\frac{x}{8x\left(x-2\right)}\)
\(\Rightarrow4\left(x-1\right)-7\left(x-2\right)=2\left(5-x\right)-x\)
\(\Leftrightarrow4x-4-7x+14=10-2x-x\)
\(\Leftrightarrow10-3x=10-3x\)
\(\Leftrightarrow-3x+3x=10-10\)
\(\Leftrightarrow0x=0\)( luôn thỏa mãn )
Vậy S = R với \(x\ne0;x\ne2\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
23 tháng 12 2022
\(\dfrac{8x^2+16x^2+8x}{4x^2+4x}\)
= \(\dfrac{24x^2+8x}{4x^2+4x}\)
= \(\dfrac{4x(6x+2)}{4x(x+1)}\)
= \(\dfrac{6x+2}{x+1}\)
JM
1
AH
Akai Haruma
Giáo viên
4 tháng 5 2020
Lời giải:
ĐK:.......
Đặt $4x^2+4x+5=a\Rightarrow 8x^2+8x+11=2a+1; 4-4x^2-4x=9-a$
PT trở thành:
$\sqrt{a}+\sqrt{2a+1}=9-a\Leftrightarrow \sqrt{a}-2+\sqrt{2a+1}-3+(a-4)=0$
$\Leftrightarrow \frac{a-4}{\sqrt{a}+2}+\frac{2(a-4)}{\sqrt{2a+1}+3}+(a-4)=0$
$\Leftrightarrow (a-4)\left(\frac{1}{\sqrt{a}+2}+\frac{2}{\sqrt{2a+1}+3}+1\right)=0$
Dễ thấy biểu thức trong ngoặc lớn luôn lớn hơn $0$ nên $a-4=0$
$\Rightarrow a=4$
$\Leftrightarrow 4x^2+4x+5=4$
$\Leftrightarrow 4x^2+4x+1=0\Leftrightarrow (2x+1)^2=0\Leftrightarrow x=-\frac{1}{2}$
\(4^x.8^x=1024\)
\(\Rightarrow32^x=1024\)
\(\Rightarrow32^2=1024\)
\(\Rightarrow x=2\)