Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
x - 512 + 1024 - x = 16 + 4 x - 512 1024 - x 8 (*), 512 ≤ x ≤ 1024
t = x - 512 1024 - x 8 ⇒ t 4 = x - 512 1024 - x ≤ x - 512 + 1024 - x 2 = 256 ⇒ 0 ≤ t ≤ 4 t = 4 ⇒ x = 768 0 ≤ t ≤ 4
=> Bình phương hai vế (*):
( t - 4 ) t 3 + 4 t 2 + 8 t - 32 = 0 ⇔ [ x ≈ 512 , 18 x ≈ 1023 , 82

Đáp án C
x − 512 + 1024 − x = 16 + 4 ( x − 512 ) ( 1024 − x ) 8 ( * ) , ( 512 ≤ x ≤ 1024 ) t = ( x − 512 ) ( 1024 − x ) 8 ⇒ t 4 = ( x − 512 ) ( 1024 − x ) ≤ x − 512 + 1024 − x 2 = 256 ⇒ 0 ≤ t ≤ 4 ⋅ t = 4 ⇒ x = 768
0 ≤ t < 4 ⇒ bình phương 2 vế (*):
⇒ ( t − 4 ) ( t 3 + 4 t 2 + 8 t − 32 ) = 0 ⇔ t ≈ 1 , 76 ⇔ x ≈ 512 , 18 x ≈ 1023 , 82

a) ĐK: x-1 khác 0 và x+1 khác 0
<=> x khác 1 và x khác -1
b) ĐK: x-2 khác 0
<=> x khác 2

*x2+bx+c=0
\(\Delta=b^2-4c=b^2-4.\left(2b-4\right)=b^2-8b+16=\left(b-4\right)^2\)=>\(\sqrt{\Delta}=\left|b-4\right|\)
Với (b-4)2=0 =>b=4 =>c=4
PT có 1 nghiệm kép: \(x_1=x_2=-2\)
Với\(\Delta=\) (b-4)2>0,PT có 2 nghiệm pb: \(x_1=\frac{-b+\left|b-4\right|}{2};x_2=\frac{-b-\left|b-4\right|}{2}\)
Với b>4 thì: \(x_1=-2;x_2=\frac{-2b+4}{2}=-b+2\)
Với b<0 thì: x1=-b+2 ; x2=-2
Vậy khi c=2b-4 và b tùy ý thì PT: x2+bx+c=0 luôn có 1 nghiệm nguyên là -2

\(a,\)\(xy+3x+2y=6\)
\(\Rightarrow xy+3x+2y+6=6+6\)
\(\Rightarrow x\left(y+3\right)+2\left(y+3\right)=12\)
\(\Rightarrow\left(y+3\right)\left(y+2\right)=12\)
\(TH1\):\(\orbr{\begin{cases}y+3=1\\x+2=12\end{cases}\Rightarrow\orbr{\begin{cases}y=-2\\x=10\end{cases}}}\)
\(TH2\): \(\orbr{\begin{cases}y+3=-1\\x+2=-12\end{cases}\Rightarrow\orbr{\begin{cases}y=-4\\x=-14\end{cases}}}\)
\(TH3\): \(\orbr{\begin{cases}y+3=12\\x+2=1\end{cases}\Rightarrow\orbr{\begin{cases}y=9\\x=-1\end{cases}}}\)
\(TH4\): \(\orbr{\begin{cases}y+3=-12\\x+2=-1\end{cases}\Rightarrow\orbr{\begin{cases}y=-15\\x=-3\end{cases}}}\)
\(TH5\): \(\orbr{\begin{cases}y+3=2\\x+2=6\end{cases}\Rightarrow\orbr{\begin{cases}y=-1\\x=4\end{cases}}}\)
\(TH6\): \(\orbr{\begin{cases}y+3=6\\x+2=2\end{cases}\Rightarrow\orbr{\begin{cases}x=3\\x=0\end{cases}}}\)
\(TH7\): \(\orbr{\begin{cases}y+3=-2\\x+2=-6\end{cases}\Rightarrow\orbr{\begin{cases}y=-5\\x=-8\end{cases}}}\)
\(TH8\)\(:\)\(\orbr{\begin{cases}y+3=-6\\x+2=-2\end{cases}\Rightarrow\orbr{\begin{cases}y=-9\\x=-4\end{cases}}}\)
\(TH9\): \(\orbr{\begin{cases}y+3=3\\x+2=4\end{cases}\Rightarrow\orbr{\begin{cases}y=0\\x=2\end{cases}}}\)
\(TH10\): \(\orbr{\begin{cases}y+3=4\\x+2=3\end{cases}\Rightarrow\orbr{\begin{cases}y=1\\x=1\end{cases}}}\)
\(TH11\): \(\orbr{\begin{cases}y+3=-3\\x+2=-4\end{cases}\Rightarrow\orbr{\begin{cases}y=-6\\x=-6\end{cases}}}\)
\(TH12\): \(\orbr{\begin{cases}y+3=-4\\x+2=-3\end{cases}\Rightarrow\orbr{\begin{cases}y=-7\\x=-5\end{cases}}}\)
KL...
chưa thấy bạn nào làm bài 3 , thì em làm ạ :))
Giả sử x, y là các số nguyên thoă mãn phương trình đã cho .
\(4x+5y=2012\Leftrightarrow5y=2012-4y\Leftrightarrow5y=4\left(503-y\right).\)(1)
Dễ thấy vế phải của (1) chia hết cho 4 \(\Rightarrow5y⋮4\)mà (5;4)=1 nên y chia hết cho 4.
Đặt \(y=4t\left(t\in Z\right)\)thế vào phương trình đầu ta được : \(4x+20t=2012\Leftrightarrow\hept{\begin{cases}x=503-5t\\y=4t\end{cases}.}\)(*)
Thử thay vào các biểu thức của x, y ở (*) ta thấy thỏa mãn
Vậy phương trình có vô số nghiệm \(\left(x;y\right)=\left(503-5t;4t\right)\forall t\in Z.\)



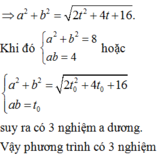
Đáp án D
Lời giải:
Đặt t = x − 512 1024 − x 8 ≥ 0 , ta có
t 4 = x − 512 1024 − x ≤ x − 512 + 1024 − x 2 = 256 ⇒ 0 ≤ t ≤ 4
Với t = 4 thì ta tìm được 1 giá trị của x = 768
Với 0 ≤ t ≤ 4 thì ta tìm được 2 giá trị của x (Khi đó phương trình của Định lý Viét đảo có 2 nghiệm phân biệt)
Bình phương 2 vế phương trình đã cho, ta được
(sử dụng máy tính).
Từ đó ta có 2 nghiệm x thỏa mãn
Do đó phương trình đã cho có 3 nghiệm.