Với số liệu đo đạc được ghi trên Hình 14, hãy tính bề rộng \(CD\) của con kênh.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có \(\widehat {ABE} = \widehat {ACD}\), mà hai góc này ở vị trí đồng vị nên \(BE//CD\).
Ta có: \(AC = AB + BC = 200 + 400 = 600m\)
Xét tam giác \(ACD\) có \(BE//CD\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{AB}}{{AC}} = \frac{{BE}}{{CD}} \Rightarrow \frac{{200}}{{600}} = \frac{{120}}{{CD}}\). Do đó, \(CD = \frac{{120.600}}{{200}} = 360\).
Vậy \(CD = 360m\).

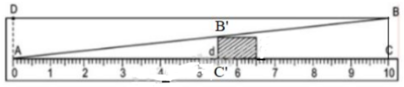
Theo hình vẽ và dựa vào định lí hai tam giác đồng dạng ta có:
ΔABC 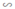 ΔAB’C’ (vì B’C’ // BC).
ΔAB’C’ (vì B’C’ // BC).
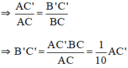
(Vì AC = 10cm, BC = 1cm).
Vậy khi đọc AC’ = 5,5cm thì bề dày của vật B’C’ = 5,5mm.
Dụng cụ trên đã dùng tính chất hai tam giác đồng dạng thì các cạnh tương ứng tỉ lệ.

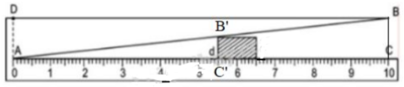
Theo hình vẽ và dựa vào định lí hai tam giác đồng dạng ta có:
ΔABC 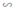 ΔAB’C’ (vì B’C’ // BC).
ΔAB’C’ (vì B’C’ // BC).
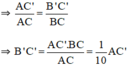
(Vì AC = 10cm, BC = 1cm).
Vậy khi đọc AC’ = 5,5cm thì bề dày của vật B’C’ = 5,5mm.
Dụng cụ trên đã dùng tính chất hai tam giác đồng dạng thì các cạnh tương ứng tỉ lệ.

Trong bảng 1: Số liệu năm 1955 so với năm 1869
Chiều rộng mặt kênh tăng: 135 – 58 = 77 (m)
Chiều rộng đáy kênh tăng: 50 – 22 = 28 (m)
Độ sâu của kênh tăng: 13 – 6 = 7 (m)
Thời gian tàu qua kênh giảm: 48 – 14 =34 (giờ)

Đáp án C
Phương pháp: Phân tích đề bài và tìm giá trị lớn nhất của cây luồng để có thể trôi qua khúc sông.
Cách giải:
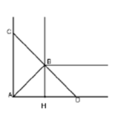
Để cây luồng có thể trôi qua khúc sông thì độ dài cây luồng không được vượt quá độ dài đoạn thẳng CD với CD là đoạn thẳng đi qua B và vuông góc với AB như hình vẽ.
Xét tam giác vuông ABH ta dễ dàng tính được . A B = 3 2
Tam giác ACD vuông tại A và có AB là phân giác đồng thời là đường cao nên Δ A C D cân tại B
AB là trung tuyến ứng với cạnh huyền.
⇒ A B = 1 2 C D ⇒ C D = 2 A B = 6 2 ≈ 8,48
Vậy trong 4 cây luồng trên chỉ có cây luồng dài 9m không trôi qua được khúc sông.
Vì \(\widehat {ABE} = \widehat {ACD} \Rightarrow BE//CD\) (hai góc đồng vị bằng nhau)
Trong tam giác \(ACD\) có \(BE//CD\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{AB}}{{AC}} = \frac{{BE}}{{CD}}\) mà \(AC = AB + BC = 8 + 8 = 16\)
Suy ra, \(\frac{8}{{16}} = \frac{3}{{CD}} \Rightarrow CD = \frac{{3.16}}{8} = 6\).
Vậy bề rộng \(CD\) của con sông là 6m.