Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

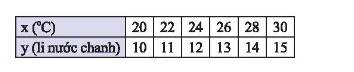
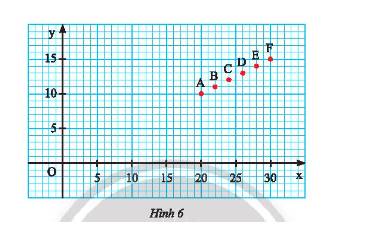
a) Điểm \(A\left( {20;10} \right);B\left( {22;11} \right);C\left( {24;12} \right);D\left( {26;13} \right);E\left( {28;14} \right);D\left( {30;15} \right)\)
Ta thấy mỗi cặp giá trị \(x;y\) tương ứng trong bảng là tọa độ của các điểm \(A;B;C;D;E;F\).

Tỉ số:
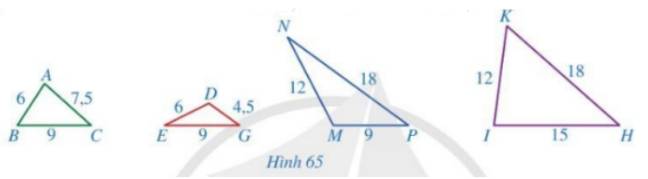
\(\frac{{DE}}{{AC}} = \frac{6}{8} = \frac{3}{4};\frac{{EF}}{{BC}} = \frac{{15}}{{20}} = \frac{3}{4}\).
Xét tam giác\(DEF\) và tam giác\(ABC\) có:
\(\frac{{DE}}{{AC}} = \frac{{EF}}{{BC}} = \frac{3}{4}\) (chứng minh trên)
Do đó, \(\Delta DEF\backsim\Delta ABC\).
Tỉ số:
\(\frac{{DE}}{{MN}} = \frac{6}{3} = 2;\frac{{EF}}{{NP}} = \frac{{15}}{6} = \frac{5}{2}\).
Vì \(\frac{{DE}}{{MN}} \ne \frac{{EF}}{{NP}}\) nên hai tam giác \(DEF\) và \(MNP\) không đồng dạng với nhau.
Tỉ số:
\(\frac{{DE}}{{RS}} = \frac{6}{4} = \frac{3}{2};\frac{{EF}}{{ST}} = \frac{{15}}{{12}} = \frac{5}{4}\).
Vì \(\frac{{DE}}{{RS}} \ne \frac{{EF}}{{ST}}\) nên hai tam giác \(DEF\) và \(SRT\) không đồng dạng với nhau.

Xét tam giác ABC và tam giác IKH có:
\(\frac{{AB}}{{IK}} = \frac{{AC}}{{IH}} = \frac{{BC}}{{KH}} = \frac{1}{2}\)
\( \Rightarrow \Delta ABC \backsim\Delta IKH\) (c-c-c)
Xét tam giác DEG và tam giác MNP có:
\(\frac{{DE}}{{MN}} = \frac{{DG}}{{MP}} = \frac{{EG}}{{KH}} = \frac{1}{2}\)
\( \Rightarrow \Delta DEG \backsim\Delta MNP\) (c-c-c)

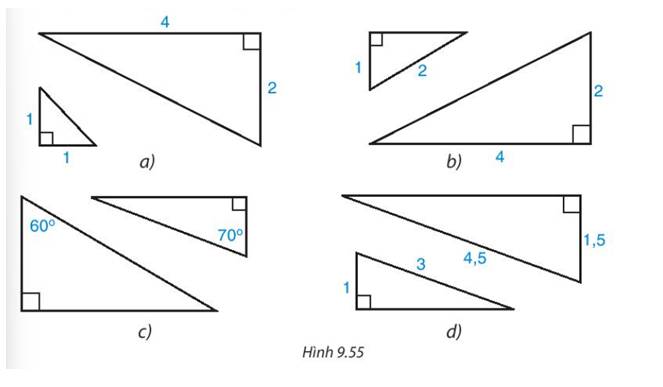
Cặp tam giác vuông ở hình d. Vì cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia

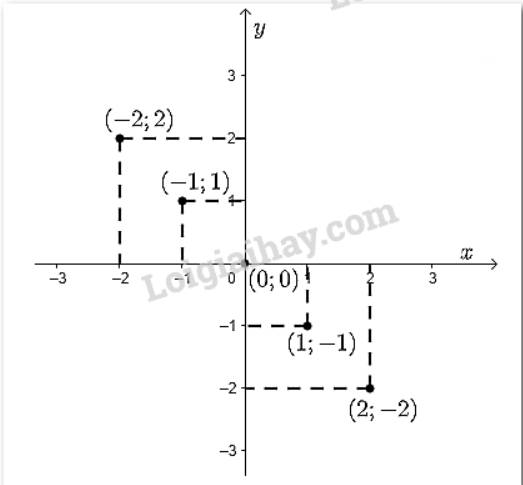
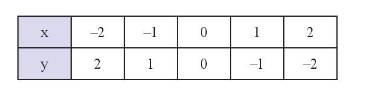
Đồ thị hàm số là tập hợp các điểm có tọa độ \(\left( { - 2;2} \right);\left( { - 1;1} \right);\left( {0;0} \right);\left( {1; - 1} \right);\left( {2; - 2} \right)\) được vẽ trên mặt phẳng tọa độ như hình dưới đây:

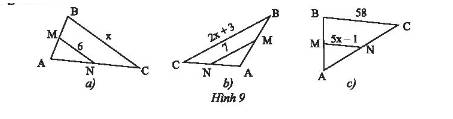
- Hình a:
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}x \Leftrightarrow 6 = \frac{1}{2}x \Leftrightarrow x = 6:\frac{1}{2} = 12\)
- Hình b:
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}\left( {x + 3} \right) \Leftrightarrow 7 = \frac{1}{2}\left( {x + 3} \right) \Leftrightarrow \left( {x + 3} \right) = 7:\frac{1}{2} = 14\)
\( \Rightarrow x = 14 - 3 \Leftrightarrow x = 11\).
- Hình c
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\[\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}.58 \Leftrightarrow \left( {5x - 1} \right) = \frac{1}{2}.58\]
\[ \Leftrightarrow \left( {5x - 1} \right) = 29 \Leftrightarrow 5x = 30 \Leftrightarrow x = 30:5 \Leftrightarrow x = 6\].
a: MN là đường trung bình
=>MN=BC/2
=>x=6*2=12
b: MN là đường trung bình
=>2x+3=2*7=14
=>2x=11
=>x=11/2
c: MN là đường trung bình
=>5x-1=58/2=29
=>5x=30
=>x=6

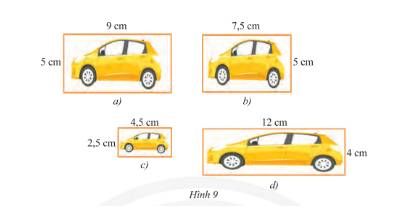
- Xét hình 9a và hình 9b ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 9a và hình 9b lần lượt là:
\(\frac{9}{{7,5}} = 1,2;\frac{5}{5} = 1\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 9a để bằng hình 9b. Do đó, hình 9a và hình 9b không đồng dạng với nhau.
- Xét hình 9a và hình 9c ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 9a và hình 9c lần lượt là:
\(\frac{9}{{4,5}} = 2;\frac{5}{{2,5}} = 2\). Do đó, tồn tại hình động dạng phối cảnh của hình 9a bằng hình 9c (hình 9a thu nhỏ với tỉ số 2). Do đó, hình 9a và hình 9c đồng dạng với nhau.
- Xét hình 9a và hình 9d ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 9a và hình 9d lần lượt là:
\(\frac{9}{{12}} = 0,75;\frac{5}{4} = 1,25\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 9a để bằng hình 9b. Do đó, hình 9a và hình 9b không đồng dạng với nhau.

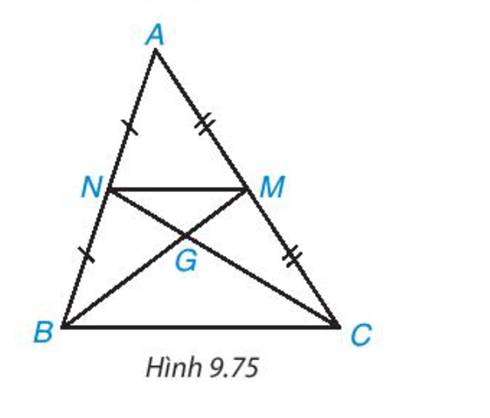
- Xét tam giác ABC có, NA=NB, MA=MC
=> NM là đường trung bình của tam giác ABC
=> NM // BC, \(NM = \frac{1}{2}AB\)
- Xét tam giác GMN và tam giác GBC có NM // BC => ΔGMN ∽ ΔGBC
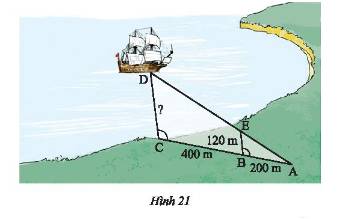



Ta có \(\widehat {ABE} = \widehat {ACD}\), mà hai góc này ở vị trí đồng vị nên \(BE//CD\).
Ta có: \(AC = AB + BC = 200 + 400 = 600m\)
Xét tam giác \(ACD\) có \(BE//CD\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{AB}}{{AC}} = \frac{{BE}}{{CD}} \Rightarrow \frac{{200}}{{600}} = \frac{{120}}{{CD}}\). Do đó, \(CD = \frac{{120.600}}{{200}} = 360\).
Vậy \(CD = 360m\).