Cho hình vuông ABCD có cạnh bằng a, M là trung điểm của BC. Tính giá trị đúng của cos AMD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


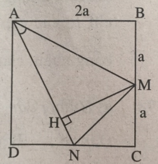
Kẻ đường cao MH của tam giác cân AMN. Ta có sin ∠ (NAM) = HM/AM và diện tích tam giác AMN là S A M N = 1/2AN.MH = 1/2AN.AM.sin(NAM) = 1/2 A N 2 .sin(NAM) = 1/2( A D 2 + D N 2 ). sin(NAM) = ( 5 a 2 )/2 sin(NAM).
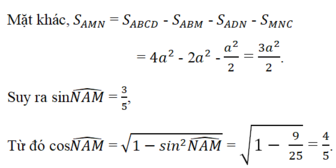

Chọn A.
Theo quy tắc hình bình hành ta có ![]()
Do đó
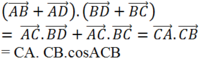
(![]() vì AC và BD vuông góc với nhau)
vì AC và BD vuông góc với nhau)
Mặt khác ![]() và theo định lý Pitago ta có:
và theo định lý Pitago ta có:
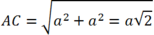
Suy ra ![]()
![]()

Nối A với C;B với D. A B D C M
Ta có:S ABC = 2/3 S ADC (vì AB=2/3 DC;chiều cao là chiều cao hình thang ABCD.)
=> S ABC=2/5 S ABCD
S ABM=1/2 S ABC( vì BM=1/2 BC;chung chiều cao hạ từ A xuống BM và BC)
S ABM = 1/2 S ABC
S ABM = 1/2(2/5 S ABCD)
S ABM = 1/5 S ABCD = 120:5=24(cm2)
Ta lại có:S BCD=3/2 S ABD(CD=3/2 AB;chiều cao là chiều cao hình thang ABCD) =>S BCD=3/5 S ABCD
S MDC=1/2 S BCD(MC=1/2 BC;chung chiều cao hạ từ đỉnh D xuống MC và BC)
S MDC=1/2 S BCD=1/2(3/5 S ABCD)=3/10 S ABCD=120:10x3=36(cm2)
S AMD=S ABCD -S MDC-S ABM=120-36-24=60(cm2)
Đ/s:AMD=60cm2;ABM=24 cm2

Chọn B
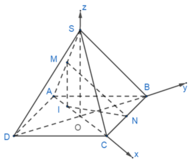
Gọi I là hình chiếu của M lên (ABCD), suy ra I là trung điểm của AO.
Khi đó
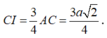
Xét tam giác CNI có
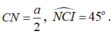
Áp dụng định lý cosin ta có:
![]()

Xét tam giác MIN vuông tại I nên
![]()
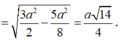
Mà MI//SO
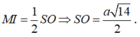
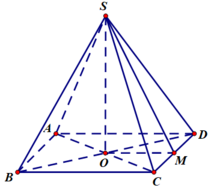
Chọn hệ trục tọa độ như hình vẽ. Ta có:
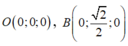
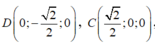
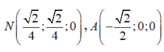
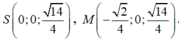
Khi đó
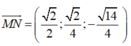
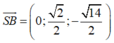
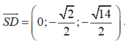
Vectơ pháp tuyến mặt phẳng (SBD)
![]()
Suy ra
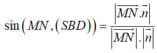
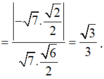


B C D A a M
Theo định lý cosin ta có
\(AD^2=AM^2+MD^2-2.MA.MD.cos\widehat{ÀMD}\)
Xé \(\Delta ABM\)có \(BM=\frac{a}{2}\)
\(AM=\sqrt{AB^2+BM^2}=\sqrt{a^2+\left(\frac{a}{2}\right)^2}=\frac{\sqrt{5}a}{2}\)
Xét \(\Delta DCM\)có \(CM=\frac{a}{2}\)
\(\Rightarrow DM=\sqrt{DC^2+CM^2}=\sqrt{a^2+\left(\frac{a}{2}\right)^2}=\frac{\sqrt{5}a}{2}\)
\(\Rightarrow\cos\widehat{AMD}=\frac{AM^2+MD^2-AD^2}{2.MA.MD}=\frac{\frac{5a^2}{4}+\frac{5a^2}{4}-a^2}{\frac{\sqrt{5}a}{2}.\frac{\sqrt{5}a}{2}}=\frac{3}{5}\)
Vậy \(\cos\widehat{AMD}=\frac{3}{5}\)
cám ơn bạn nha