Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

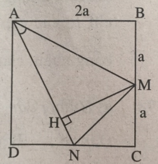
Kẻ đường cao MH của tam giác cân AMN. Ta có sin ∠ (NAM) = HM/AM và diện tích tam giác AMN là S A M N = 1/2AN.MH = 1/2AN.AM.sin(NAM) = 1/2 A N 2 .sin(NAM) = 1/2( A D 2 + D N 2 ). sin(NAM) = ( 5 a 2 )/2 sin(NAM).
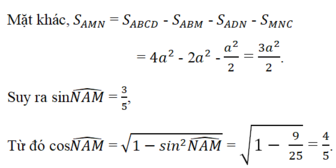

b: MD*MC=MH*DC=2*a
a: Xet ΔBEC vuông tại B và ΔCFD vuông tại C có
BE=CF
BC=CD
=>ΔBEC=ΔCFD
=>góc BEC=góc CFD
=>góc CFD+góc FCM=90 độ
=>CE vuông góc BD
Xét ΔDMC vuông tại D và ΔCBE vuông tại B có
góc MCD=góc BEC
=>ΔDMC đồng dạng với ΔCBE
\(S_{CBE}=\dfrac{1}{2}\cdot S_{BAC}=\dfrac{1}{4}\cdot S_{ABCD}\)
ΔDMC đồng dạng với ΔCBE
=>\(\dfrac{S_{DMC}}{S_{CBE}}=\left(\dfrac{DC}{CE}\right)^2=\left(\dfrac{2\cdot BE}{\sqrt{\left(2\cdot BE\right)^2+BE^2}}\right)^2=\left(\dfrac{2}{\sqrt{5}}\right)^2=\dfrac{4}{5}\)
=>\(S_{DMC}=\dfrac{4}{5}\cdot S_{CBE}=\dfrac{4}{5}\cdot\dfrac{1}{4}\cdot S_{ABCD}=\dfrac{1}{5}\cdot S_{ABCD}\)

A B C D F E M
Xét tam giác vuông là tam giác BEC và tam giác DCF có CD = BC , BE = CF = 1/2a
=> Tam giác BEC = tam giác DCF (hai cạnh góc vuông)
=> góc CDF = góc BCE mà góc CDF + góc DFC = 90 độ
=> góc ECF + góc DFC = 90 độ hay góc DMC = 90 độ => CE vuông góc DF
Ta chứng minh được tam giác MDC đồng dạng tam giác CDF (g.g)
Áp dụng định lí Pytago có \(DF=\sqrt{CD^2+FC^2}=\sqrt{a^2+\frac{a^2}{4}}=\frac{a\sqrt{5}}{2}\)
\(S_{CDF}=\frac{1}{2}CD.CF=\frac{1}{2}a.\left(\frac{a}{2}\right)=\frac{a^2}{4}\)
Suy ra \(\frac{S_{MDC}}{S_{CDF}}=\left(\frac{CD}{DF}\right)^2=\left(\frac{a}{\frac{a\sqrt{5}}{2}}\right)^2=\left(\frac{2}{\sqrt{5}}\right)^2=\frac{4}{5}\)
\(\Rightarrow S_{MDC}=\frac{4}{5}S_{CDF}=\frac{4}{5}.\frac{a^2}{4}=\frac{a^2}{5}\)

Vì \(\tan MAB=\frac{MB}{AB}=\frac{1}{2}\Rightarrow\widehat{MAB}=26,5°\)Tương tự có \(\widehat{NAD}=26,5°\)
\(\Rightarrow\widehat{MAN}=37°\Rightarrow\cos MAN=\cos37\approx0,79\)

Đặt cạnh hình vuông là a
Dễ tính được: \(AN=\sqrt{AD^2+DN^2}=\dfrac{a\sqrt{5}}{2}\), \(MN=\sqrt{MC^2+CN^2}=\sqrt{\left(\dfrac{a}{2}\right)^2+\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{2}}{2}\)
\(AM=\sqrt{AB^2+BM^2}=\sqrt{a^2+\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{5}}{2}\)
Kẻ \(MK\perp AN\)
Ta chứng minh: \(cos\widehat{ANM}=\dfrac{AN^2+MN^2-AM^2}{2AN.NM}\) (1)
(1) \(\Leftrightarrow2AN.MN.cos\widehat{N}=AN^2+MN^2-AM^2\)
\(\Leftrightarrow2.AN.MN.\dfrac{KN}{MN}=\left(AK+KN\right)^2+MK^2+NK^2-MK^2-AK^2\)
\(\Leftrightarrow2.AN.KN=AK^2+2.AK.KN+KN^2+NK^2-AK^2\)
\(\Leftrightarrow2KN.AK-2AN.NK+2KN^2=0\)
\(\Leftrightarrow2KN\left(AK-AN+KN\right)=0\) \(\Leftrightarrow2.KN.0=0\) (lđ)
Từ (1) \(\Rightarrow cos\widehat{ANM}=\dfrac{\left(\dfrac{a\sqrt{5}}{2}\right)^2+\left(\dfrac{a\sqrt{2}}{2}\right)^2-\left(\dfrac{a\sqrt{5}}{2}\right)^2}{2.\left(\dfrac{a\sqrt{5}}{2}\right)\left(\dfrac{a\sqrt{2}}{2}\right)}\)\(=\dfrac{\sqrt{10}}{10}\)
Ý B

B C D A a M
Theo định lý cosin ta có
\(AD^2=AM^2+MD^2-2.MA.MD.cos\widehat{ÀMD}\)
Xé \(\Delta ABM\)có \(BM=\frac{a}{2}\)
\(AM=\sqrt{AB^2+BM^2}=\sqrt{a^2+\left(\frac{a}{2}\right)^2}=\frac{\sqrt{5}a}{2}\)
Xét \(\Delta DCM\)có \(CM=\frac{a}{2}\)
\(\Rightarrow DM=\sqrt{DC^2+CM^2}=\sqrt{a^2+\left(\frac{a}{2}\right)^2}=\frac{\sqrt{5}a}{2}\)
\(\Rightarrow\cos\widehat{AMD}=\frac{AM^2+MD^2-AD^2}{2.MA.MD}=\frac{\frac{5a^2}{4}+\frac{5a^2}{4}-a^2}{\frac{\sqrt{5}a}{2}.\frac{\sqrt{5}a}{2}}=\frac{3}{5}\)
Vậy \(\cos\widehat{AMD}=\frac{3}{5}\)
cám ơn bạn nha