Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì \(\tan MAB=\frac{MB}{AB}=\frac{1}{2}\Rightarrow\widehat{MAB}=26,5°\)Tương tự có \(\widehat{NAD}=26,5°\)
\(\Rightarrow\widehat{MAN}=37°\Rightarrow\cos MAN=\cos37\approx0,79\)

A B C D M N 2a H
a) Gọi H là giao điểm của AM và BN
\(\Delta ABMvà\Delta BCN\) có:
AB=BC(ABCD là hình vuông)
góc ABM=góc BCN=90o
BM=CN=1/2 cạnh hình vuông
=>\(\Delta ABM=\Delta BCN\left(c-g-c\right)\)
=> góc AMB= góc BNC
mà BNC+HBC=90o
=>AMB+HBC=900
=> góc BHM=900
=>\(AM\perp BN\)(đpcm)
b)tam giác ABM và tam giác ADN có:
AB=AD(ABCD là hình vuông )
góc ABM=góc ADN=90o
BM=DN=1/2 cạnh hình vuông
=> tam giác ABM= tam giác ADN(c.g.c)
=> AM=AN=\(\sqrt{AD^2+DN^2}=\sqrt{\left(2DN\right)^2+DN^2}=DN\sqrt{5}=a\sqrt{5}\)
tam giác ABH vuông tại B có BH vuông góc với AM
=> AH.AM=AB2
\(\Rightarrow AH=\dfrac{AB^2}{AM}=\dfrac{4a^2}{a\sqrt{5}}=\dfrac{4a}{\sqrt{5}}\)
=> cos MAN = \(\dfrac{AH}{AN}=\dfrac{4a}{\sqrt{5}}:a\sqrt{5}=\dfrac{4}{5}\)

A B C D F E M
Xét tam giác vuông là tam giác BEC và tam giác DCF có CD = BC , BE = CF = 1/2a
=> Tam giác BEC = tam giác DCF (hai cạnh góc vuông)
=> góc CDF = góc BCE mà góc CDF + góc DFC = 90 độ
=> góc ECF + góc DFC = 90 độ hay góc DMC = 90 độ => CE vuông góc DF
Ta chứng minh được tam giác MDC đồng dạng tam giác CDF (g.g)
Áp dụng định lí Pytago có \(DF=\sqrt{CD^2+FC^2}=\sqrt{a^2+\frac{a^2}{4}}=\frac{a\sqrt{5}}{2}\)
\(S_{CDF}=\frac{1}{2}CD.CF=\frac{1}{2}a.\left(\frac{a}{2}\right)=\frac{a^2}{4}\)
Suy ra \(\frac{S_{MDC}}{S_{CDF}}=\left(\frac{CD}{DF}\right)^2=\left(\frac{a}{\frac{a\sqrt{5}}{2}}\right)^2=\left(\frac{2}{\sqrt{5}}\right)^2=\frac{4}{5}\)
\(\Rightarrow S_{MDC}=\frac{4}{5}S_{CDF}=\frac{4}{5}.\frac{a^2}{4}=\frac{a^2}{5}\)

Chi tiết \(BM=DN=\dfrac{a}{3}\) hoàn toàn không cần thiết
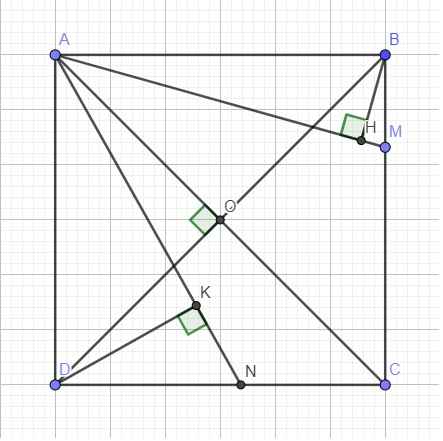
a.
Ta có: \(AC\perp BD\) tại O (2 đường chéo hình vuông) \(\Rightarrow O\) thuộc đường tròn đường kính AB
\(AH\perp BH\) (gt) \(\Rightarrow\) H thuộc đường tròn đường kính AB
\(\Rightarrow\) 4 điểm A,B,O,H cùng thuộc đường tròn đường kính AB hay tứ giác ABHO nội tiếp
Hoàn toàn tương tự, 4 điểm ADKO cùng thuộc đường tròn đường kính AD nên tứ giác ADKO nội tiếp
b.
Trong tam giác vuông ABM vuông tại B với đường cao BH, áp dụng hệ thức lượng:
\(AB^2=AH.AM\)
Tương tự, trong tam giác vuông ADN:
\(AD^2=AK.AN\)
Mà \(AB=AD=a\Rightarrow AH.AM=AK.AN\Rightarrow\dfrac{AH}{AN}=\dfrac{AK}{AM}\) (đpcm)

Kẻ đường cao MH của tam giác cân AMN. Ta có sin ∠ (NAM) = HM/AM và diện tích tam giác AMN là S A M N = 1/2AN.MH = 1/2AN.AM.sin(NAM) = 1/2 A N 2 .sin(NAM) = 1/2( A D 2 + D N 2 ). sin(NAM) = ( 5 a 2 )/2 sin(NAM).