cho \(cosx\) = \(-\dfrac{2}{3}\) tính giá trị của \(cos2x\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 12 2023
1: \(P=sin^22x=1-cos^22x\)
\(=1-\left(cos2x\right)^2\)
\(=1-\left(2cos^2x-1\right)^2\)
\(=1-\left(2\cdot\dfrac{9}{16}-1\right)^2\)
\(=1-\left(\dfrac{9}{8}-1\right)^2=1-\left(\dfrac{1}{8}\right)^2=\dfrac{63}{64}\)
2:
\(cos2x-sin\left(x+\dfrac{\Omega}{3}\right)=0\)
=>\(sin\left(x+\dfrac{\Omega}{3}\right)=cos2x=sin\left(\dfrac{\Omega}{2}-2x\right)\)
=>\(\left[{}\begin{matrix}x+\dfrac{\Omega}{3}=\dfrac{\Omega}{2}-2x+k2\Omega\\x+\dfrac{\Omega}{3}=\Omega-\dfrac{\Omega}{2}+2x+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}3x=\dfrac{\Omega}{6}+k2\Omega\\-x=\dfrac{1}{6}\Omega+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Omega}{18}+\dfrac{k2\Omega}{3}\\x=-\dfrac{1}{6}\Omega-k2\Omega\end{matrix}\right.\)
9 tháng 7 2021
Tính tổng các giá trị của m trên đoạn \(\left[-\dfrac{\pi}{3};\dfrac{\pi}{2}\right]\) có nghĩa là \(x\in\left[-\dfrac{\pi}{3};\dfrac{\pi}{2}\right]\) pk?
\(\Rightarrow cosx\in\left[0;1\right]\)
\(y=2cos^2x+cosx-1+\left|2m-1\right|\)
Đặt \(t=cosx;t\in\left[0;1\right]\)
\(y=2t^2+t-1+\left|2m-1\right|\)
Xét BBT của \(f\left(t\right)=2t^2+t-1;t\in\left[0;1\right]\)
\(\Rightarrow f\left(t\right)_{min}=-1\Leftrightarrow t=0\Leftrightarrow cosx=0\)\(\Leftrightarrow x=\dfrac{\pi}{2}\)
\(\Rightarrow y\ge-1+\left|2m-1\right|\)
Để \(y_{min}=2\Leftrightarrow-1+\left|2m-1\right|=2\)\(\Leftrightarrow m=2;m=-1\)
\(\Rightarrow\)Tổng m bằng \(1\)
PT
1
CM
7 tháng 2 2018
Ta có : sin2 x + cos2 x = 1 ⇒ sin2 x = 1 – cos2 x.
⇒ P = 3.sin2 x + cos2 x
= 3.(1 – cos2x) + cos2 x
= 3 – 3.cos2x + cos2x
= 3 – 2.cos2x
= 3 – 2.(1/3)2
= 3 – 2/9
= 25/9.
MA
1
17 tháng 5 2021
\(cosx=\dfrac{4}{5}\Rightarrow cos^2x=\dfrac{16}{25}\)
\(\Rightarrow sin^2x=1-cos^2x=1-\dfrac{16}{25}=\dfrac{9}{25}\)
\(\Rightarrow\sqrt{cos2x}=\sqrt{cos^2x-sin^2x}=\sqrt{\dfrac{16}{25}-\dfrac{9}{25}}=\sqrt{\dfrac{7}{25}}=\dfrac{\sqrt{7}}{5}\)
Em mới lớp 8 nên làm không chắc nhé anh/chị.
CM
1 tháng 4 2017
Đáp án C
Áp dụng bất đẳng thức Bunhiacopxki ta có
Suy ra 
Giá trị y = 2 đặt được khi 
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 7 2021
1.
\(0< x< \dfrac{\pi}{2}\Rightarrow cosx>0\)
\(\Rightarrow cosx=\sqrt{1-sin^2x}=\dfrac{\sqrt{5}}{3}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{2}{\sqrt{5}}\)
\(sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\left(sinx+cosx\right)=\dfrac{\sqrt{10}+2\sqrt{2}}{6}\)
2.
Đề bài thiếu, cos?x
Và x thuộc khoảng nào?
3.
\(x\in\left(0;\dfrac{\pi}{2}\right)\Rightarrow sinx;cosx>0\)
\(\dfrac{1}{cos^2x}=1+tan^2x=5\Rightarrow cos^2x=\dfrac{1}{5}\Rightarrow cosx=\dfrac{\sqrt{5}}{5}\)
\(sinx=cosx.tanx=\dfrac{2\sqrt{5}}{5}\)
4.
\(A=\left(2cos^2x-1\right)-2cos^2x+sinx+1=sinx\)
\(B=\dfrac{cos3x+cosx+cos2x}{cos2x}=\dfrac{2cos2x.cosx+cos2x}{cos2x}=\dfrac{cos2x\left(2cosx+1\right)}{cos2x}=2cosx+1\)
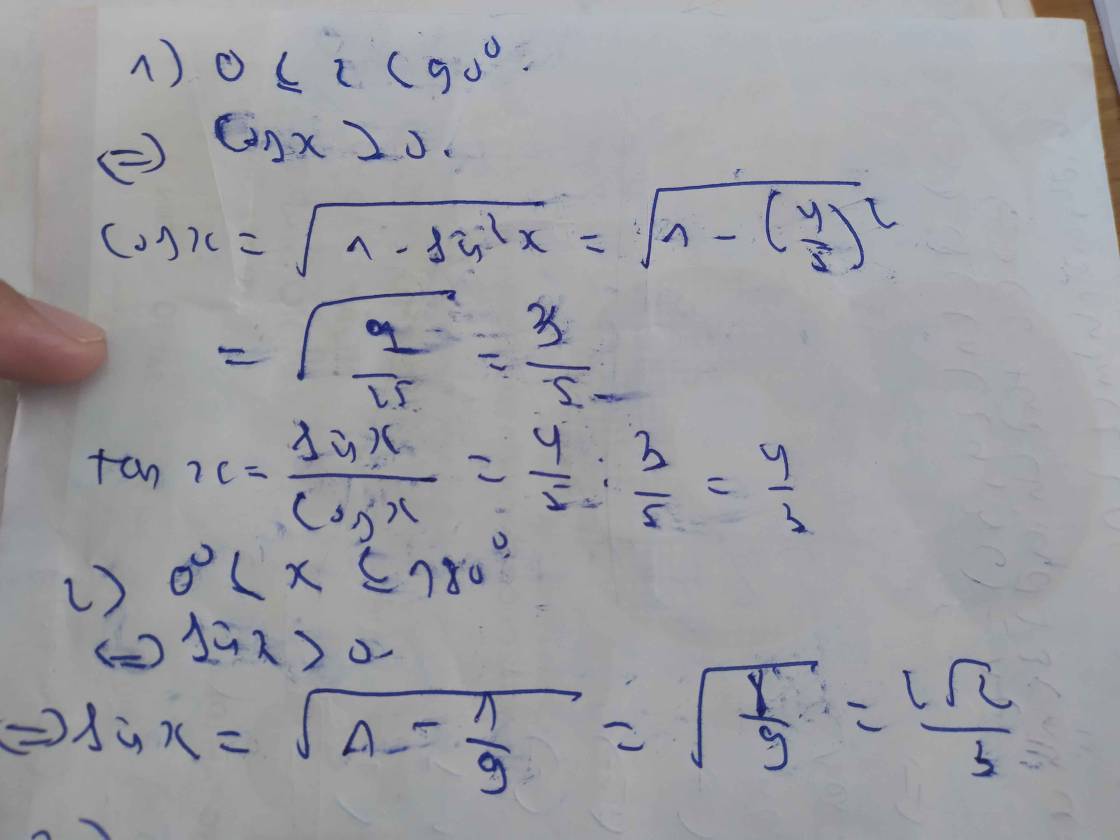
\(cos2x=2\cdot cos^2x-1=2\cdot\dfrac{4}{9}-1=-\dfrac{1}{9}\)