MA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 7 2021
Tính tổng các giá trị của m trên đoạn \(\left[-\dfrac{\pi}{3};\dfrac{\pi}{2}\right]\) có nghĩa là \(x\in\left[-\dfrac{\pi}{3};\dfrac{\pi}{2}\right]\) pk?
\(\Rightarrow cosx\in\left[0;1\right]\)
\(y=2cos^2x+cosx-1+\left|2m-1\right|\)
Đặt \(t=cosx;t\in\left[0;1\right]\)
\(y=2t^2+t-1+\left|2m-1\right|\)
Xét BBT của \(f\left(t\right)=2t^2+t-1;t\in\left[0;1\right]\)
\(\Rightarrow f\left(t\right)_{min}=-1\Leftrightarrow t=0\Leftrightarrow cosx=0\)\(\Leftrightarrow x=\dfrac{\pi}{2}\)
\(\Rightarrow y\ge-1+\left|2m-1\right|\)
Để \(y_{min}=2\Leftrightarrow-1+\left|2m-1\right|=2\)\(\Leftrightarrow m=2;m=-1\)
\(\Rightarrow\)Tổng m bằng \(1\)
AH
Akai Haruma
Giáo viên
18 tháng 8 2021
Lời giải:
$-\frac{4}{5}=\cos 2x=2\cos ^2x-1$
$\Leftrightarrow \cos ^2x=\frac{1}{10}$
Vì $x\in (\frac{\pi}{4}; \frac{\pi}{2})$ nên $\cos x>0$
$\Rightarrow \cos x=\sqrt{\frac{1}{10}}$
$\sin^2x=1-\cos ^2x=\frac{9}{10}$
Vì $x\in (\frac{\pi}{4}; \frac{\pi}{2})$ nên $\sin x>0$
$\Rightarrow \sin x=\frac{3}{\sqrt{10}}$
$\sin (x+\frac{\pi}{3})=\sin x\cos \frac{\pi}{3}+\cos x\sin \frac{\pi}{3}$
$=\sqrt{\frac{9}{10}}.\frac{1}{2}+\sqrt{\frac{1}{10}}.\frac{\sqrt{3}}{2}=\frac{\sqrt{30}+3\sqrt{10}}{20}$
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 12 2020
\(m+3\sqrt[3]{m+3cosx}=cos^3x\)
Đặt \(\sqrt[3]{m+3cosx}=t\Rightarrow m=t^3-3cosx\)
\(\Rightarrow t^3-3cosx+3t=cos^3x\)
\(\Leftrightarrow t^3+3t=cos^3x+3cosx\)
Hàm \(f\left(t\right)=t^3+3t\) có \(f'\left(t\right)=3t^2+3>0\Rightarrow f\left(t\right)\) đồng biến
\(\Rightarrow t=cosx\) (hoặc là bạn liên hợp cũng được, tùy thích)
\(\Leftrightarrow m=t^3-3cosx=cos^3x-3cosx\)
Đặt \(cosx=u\in\left[-1;1\right]\Rightarrow f\left(u\right)=u^3-3u=m\)
Xét hàm \(f\left(u\right)=u^3-3u\) trên \(\left[-1;1\right]\)
\(f'\left(u\right)=3u^2-3\Rightarrow u=\pm1\)
\(f\left(-1\right)=2\) ; \(f\left(1\right)=-2\Rightarrow-2\le f\left(u\right)\le2\)
\(\Rightarrow-2\le m\le2\)
DN
1
18 tháng 1 2022
Lần sau bạn vào cái hình E để gửi câu hỏi nha!
\(P=\dfrac{sin^2\alpha-sin\alpha\cdot cos\alpha+2cos^2\alpha}{2sin^2\alpha-cos^2\alpha}\)
\(P=\dfrac{tan^2\alpha-tan\alpha+2}{2tan^2\alpha-1}\) (Chia cả tử và mẫu cho \(cos^2\alpha\))
\(P=\dfrac{3^2-3+2}{2\cdot3^2-1}=\dfrac{8}{17}\)
Chúc bn học tốt!
PT
1
CM
7 tháng 2 2018
Ta có : sin2 x + cos2 x = 1 ⇒ sin2 x = 1 – cos2 x.
⇒ P = 3.sin2 x + cos2 x
= 3.(1 – cos2x) + cos2 x
= 3 – 3.cos2x + cos2x
= 3 – 2.cos2x
= 3 – 2.(1/3)2
= 3 – 2/9
= 25/9.
16 tháng 3 2022
\(\sin^2x=\sqrt{1-\left(-\dfrac{4}{5}\right)^2}=\dfrac{9}{25}\)
mà \(\sin x>0\)
nên \(\sin x=\dfrac{3}{5}\)
=>\(\tan x=-\dfrac{3}{4}\)
\(\Leftrightarrow\cot x=-\dfrac{4}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2021
\(P=sin^22x-\left[2sin\dfrac{x}{2}cos\dfrac{x}{2}\left(cos^4\dfrac{x}{2}-sin^4\dfrac{x}{2}\right)\right]^2\)
\(=sin^22x-\left[sinx\left(cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}\right)\left(cos^2\dfrac{x}{2}+sin^2\dfrac{x}{2}\right)\right]^2\)
\(=sin^22x-\left[sinx.cosx.1\right]^2\)
\(=sin^22x-\left[\dfrac{1}{2}sin2x\right]^2\)
\(=\dfrac{3}{4}sin^22x=\dfrac{3}{4}\left(1-cos^22x\right)=\dfrac{3}{4}\left(1-\dfrac{1}{4}\right)=\dfrac{9}{16}\)
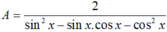
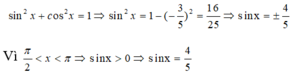
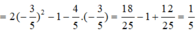
\(cosx=\dfrac{4}{5}\Rightarrow cos^2x=\dfrac{16}{25}\)
\(\Rightarrow sin^2x=1-cos^2x=1-\dfrac{16}{25}=\dfrac{9}{25}\)
\(\Rightarrow\sqrt{cos2x}=\sqrt{cos^2x-sin^2x}=\sqrt{\dfrac{16}{25}-\dfrac{9}{25}}=\sqrt{\dfrac{7}{25}}=\dfrac{\sqrt{7}}{5}\)
Em mới lớp 8 nên làm không chắc nhé anh/chị.