Cho tam giác ABC vuông tại B . Các điểm E, F là trung điểm AB , BC . Kẻ Ex song song với BC. a) Chứng minh tứ giác BMEF là hình chữ nhật b)Gọi K đối xứng với B qua E. Tứ giác BAKC là hình gì? c)Gọi G đối xứng với E qua F.Tứ giác BGCE là hình gì? d) Tam giác ABC cần thêm điều kiện gì để tứ giác BGCE là hình...
Đọc tiếp
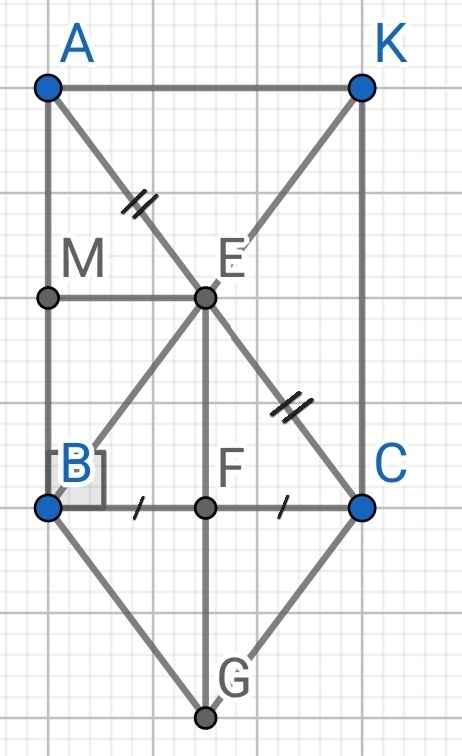
Cho tam giác ABC vuông tại B . Các điểm E, F là trung điểm AB , BC . Kẻ Ex song song với BC. a) Chứng minh tứ giác BMEF là hình chữ nhật b)Gọi K đối xứng với B qua E. Tứ giác BAKC là hình gì? c)Gọi G đối xứng với E qua F.Tứ giác BGCE là hình gì? d) Tam giác ABC cần thêm điều kiện gì để tứ giác BGCE là hình vuông?
a: Sửa đề: Ex//BC, Ex cắt AC tại M
a: Xét ΔABC có
E là trung điểm của BA
EM//BC
=>M là trung điểm của AC
Xét ΔCAB có
E,M lần lượt là trung điểm của AB,AC
=>EM là đường trung bình
=>EM=1/2BC
=>EM=BF
Xét tứ giác EMFB có
EM//FB
EM=FB
góc FBE=90 độ
Do đó: EMFB là hình chữ nhật
b: Sửa đề: K đối xứng B qua M
Xét tứ giác BAKC có
M là trung điểm chung của BK và AC
góc ABC=90 độ
=>BAKC là hình chữ nhật
c: Xét tứ giác BGCE có
F là trung điểm chung của BC và GE
=>BGCE là hình bình hành