Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

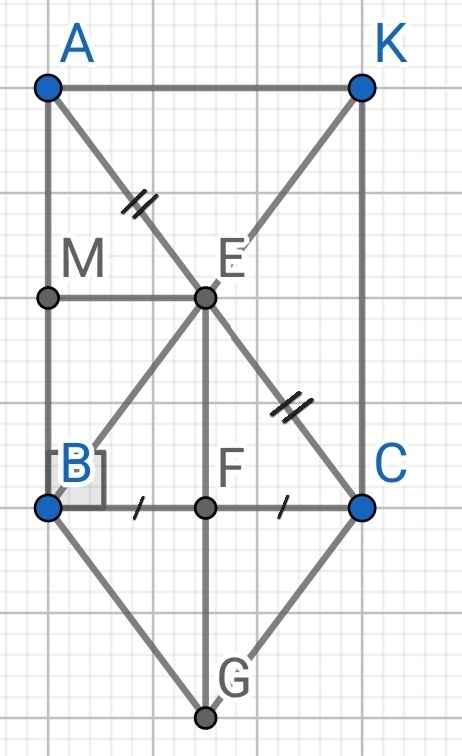
a) ∆ABC vuông tại B (gt)
⇒ AB ⊥ BC
⇒ BM ⊥ BF
⇒ ∠MBF = 90⁰
Do EM // BC (gt)
⇒ EM // BF
EM // BC (gt)
E là trung điểm của AC (gt)
⇒ M là trung điểm của AB
⇒ EM là đường trung bình của ∆ABC
⇒ EM = BC : 2
F là trung điểm của BC (gt)
⇒ BF = CF = BC : 2
⇒ EM = BF = BC : 2
Tứ giác BMEF có:
EM // BF (cmt)
EM = BF = BC : 2 (cmt)
⇒ BMEF là hình bình hành
Mà ∠MBF = 90⁰ (cmt)
⇒ BMEF là hình chữ nhật
b) Do K đối xứng với B qua E (gt)
⇒ E là trung điểm của BK
Tứ giác BAKC có:
E là trung điểm của BK (cmt)
E là trung điểm của AC (gt)
⇒ BAKC là hình bình hành
Mà ∠ABC = 90⁰ (gt)
⇒ BAKC là hình chữ nhật
c) Do G đối xứng với E qua F (gt)
⇒ F là trung điểm của EG
∆ABC vuông tại B (gt)
E là trung điểm của AC (gt)
⇒ BE là đường trung tuyến ứng với cạnh huyền AC
⇒ BE = CE = AC : 2
Tứ giác BGCE có:
F là trung điểm của BC (gt)
F là trung điểm của EG (cmt)
⇒ BGCE là hình bình hành
Mà BE = CE (cmt)
⇒ BGCE là hình thoi
d) Để BGCE là hình vuông thì BE ⊥ CE
⇒ BE là đường cao của ∆ABC
Mà BE là đường trung tuyến của ∆ABC (cmt)
⇒ ∆ABC cân tại B
Lại có ∆ABC vuông tại B (gt)
⇒ ∆ABC vuông cân tại B
\(a,\left\{{}\begin{matrix}BF=CF\\CE=EA\end{matrix}\right.\Rightarrow EF\) là đtb tam giác ABC
\(\Rightarrow EF=\dfrac{1}{2}AB;EF//AB\Rightarrow EF//BM\)
Mà \(ME//BF\) nên BMEF là hbh
Mà \(\widehat{ABC}=90^0\) nên BMEF là hcn
\(b,\left\{{}\begin{matrix}BE=EK\\AE=EC\\\widehat{ABC}=90^0\end{matrix}\right.\Rightarrow BAKC\) là hcn
\(c,\left\{{}\begin{matrix}EF=FG\\CF=BF\end{matrix}\right.\Rightarrow BGCE\) là hbh
Mà \(CE=BE\left(t/c.hình.chữ.nhật.BAKC\right)\)
Vậy BGCE là hình thoi
\(d,BGCE\) là hình vuông \(\Leftrightarrow\widehat{CEB}=90^0\Leftrightarrow CE\perp BE\)
\(\Leftrightarrow BE\) là đường cao tam giác ABC
Mà BE là trung tuyến tam giác ABC
Do đó tam giác ABC phải vuông cân
Vậy BGCE là hình vuông \(\Leftrightarrow\) tam giác ABC vuông cân

A F E D B C M
Mình vẽ hình hơi xâu, bạn thông cảm nhé!
a) Xét từ giác ABMC có: + AM cắt BC tại D (bạn dùng ký hiệu giao nhé)
+ DA = DM (gt)
+ DB = DM(gt)
suy ra, tứ giác AMCM là hình bình hành mà ta có góc CAB là góc vuông suy ra tứ giác ABMC là hình chữ nhật
Các câu còn lại bạn đầu có thể giải theo cách trên nhé!
( e mk chưa làm đc, mk mới đc học đến bào hình chữ nhật thôi, sory)

https://lazi.vn/edu/exercise/cho-tam-giac-abc-goi-d-e-f-theo-thu-tu-la-trung-diem-cua-ab-bc-ca-goi-m-n-p-q-theo-thu-tu-la-trung-diem
Bạn xem tại link này nhé
Học tốt!!!!!!

\(a,\) M,E là trung điểm BC,AB nên ME là đtb \(\Delta ABC\)
Do đó \(ME//AC\Rightarrow ME\bot AB(AC\bot AB)\)
\(b,\) Vì E là trung điểm MH và AB nên AMBH là hbh
Mà \(MH\bot AB\) tại E nên AMBH là hình thoi
\(c,\) Để \(AMBH\) là hv thì \(\widehat{AMB}=90^0\Leftrightarrow AM\bot BC\)
Mà AM là trung tuyến ứng cạnh huyền
Vậy để \(AMBH\) là hv thì \(\Delta ABC\) vuông cân tại A

Answer:
Mình chỉ biết làm a, b còn c, d mình không biết. Bạn thông cảm ạ.
 a. Có: DM vuông góc với AC; DN vuông góc với BC; AC vuông góc với BC
a. Có: DM vuông góc với AC; DN vuông góc với BC; AC vuông góc với BC
=> CMDN là hình chữ nhật
b. Xét tam giác abc VUÔNG TẠI a:
D là trung điểm AB
=> CD là đường trung tuyến
=> CD = DB = AD
=> Tam giác CDB cân tại D
Mà DN vuông góc với BC
=> DN là đường cao và cũng là trung tuyến
=> CN = NB
Xét tứ giác DCEB:
CN = NB
DN = NE
Mà DE vuông góc BC
=> Tứ giác DCEB là hình thoi.
c) Xét tam giác \(ABC\)vuông tại \(C\)có:
\(AB^2=AC^2+BC^2\)(định lí Pythagore)
\(\Leftrightarrow AC^2=AB^2-BC^2=10^2-6^2=64=8^2\)
suy ra \(AC=8\left(cm\right)\).
\(DM\)vuông góc với \(AC\)mà \(AB\perp AC\)suy ra \(DM//AB\)
mà ta lại có \(D\)là trung điểm của \(AB\)
nên \(DM\)là đường trung bình của tam giác \(ABC\).
Suy ra \(DM=\frac{1}{2}BC=\frac{1}{2}.6=3\left(cm\right)\)
Tương tự ta cũng suy ra \(DN=\frac{1}{2}AC=4\left(cm\right)\).
\(S_{CMDN}=DM.DN=3.4=12\left(cm^2\right)\).
d)
Có \(CDBE\)là hình thoi nên để \(CDBE\)là hình vuông thì \(CD\perp BE\).
Xét tam giác \(ABC\)có \(D\)là trung điểm \(AB\)mà \(CD\perp BE\)nên tam giác \(ABC\)cân tại \(C\).
Vậy tam giác \(ABC\)vuông cân tại \(C\).

a)tứ giác ABMC là hình chữ nhật (vì là hbh có 1 góc vuông)
b)Xét tam giác ABC có:BE=AE,DB=DC=>ED là đường trung bình của tam giác ABC
=>ED//AC=>ED//AF (1)
C/M tương tự DF//AE(DF là đường trung bình của tam giác BAC) (2)
Từ (1),và (2)=>EDFA là hbh.Mà BAC^=90độ=>EDFA là hcn(hbh có 1 góc vuông)
d)ĐK:tam giác ABC là tam giác cân=>AB=AC (4)
Vì AE=1/2AB,AF=1/2AC (5)
Từ (4) và (5)=>AE=AF=>ADEF là hình vuông(vì AEDF mik đã c/m là hcn ở ý b rồi)(hcn có 2 cạnh kề bắng nhau là hình vuông)
a: Sửa đề: Ex//BC, Ex cắt AC tại M
a: Xét ΔABC có
E là trung điểm của BA
EM//BC
=>M là trung điểm của AC
Xét ΔCAB có
E,M lần lượt là trung điểm của AB,AC
=>EM là đường trung bình
=>EM=1/2BC
=>EM=BF
Xét tứ giác EMFB có
EM//FB
EM=FB
góc FBE=90 độ
Do đó: EMFB là hình chữ nhật
b: Sửa đề: K đối xứng B qua M
Xét tứ giác BAKC có
M là trung điểm chung của BK và AC
góc ABC=90 độ
=>BAKC là hình chữ nhật
c: Xét tứ giác BGCE có
F là trung điểm chung của BC và GE
=>BGCE là hình bình hành