Cho hình thang cân ABCD có AB // CD, \(\widehat A = {80^o}\). Khi đó, \(\widehat C\) bằng:
A. 80o
B. 90o
C. 100o
D. 110o
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc A-góc D=20 độ
góc A+góc D=180 độ
=>góc A=(20+180)/2=100 độ và góc D=180-100=80 độ
góc B=2*góc C
góc B+góc C=180 độ
=>góc B=2/3*180=120 độ; góc C=180-120=60 độ
b: góc B-góc C=20 độ
góc B+góc C=180 độ
=>góc B=(180+20)/2=100 độ và góc C=80 độ
=>góc A=100+20=120 độ
=>góc D=60 độ

Kẻ BE // AD ; E ∈ CD ⇒ ABED là hình bình hành
⇒ \(\widehat{D}=\widehat{ABE}\) \(;\) \(\widehat{A}=\widehat{BED}\)
Ta có: \(\widehat{A}=\widehat{BED}>\widehat{C}\) \(;\) \(\widehat{ABC}=\widehat{ABE}=\widehat{D}\)
Suy ra: \(\widehat{A}+\widehat{B}>\widehat{C}+\widehat{D}\) ( đpcm )
Kẻ H // AD,H\(\in\)CD \(\Rightarrow\) ABHD là hình bình hành
\(\Rightarrow\)\(\widehat{ABH}=\widehat{D}\) ; \(\widehat{BHD}=\widehat{A}\)
Ta có:
\(\widehat{BHD}=\widehat{A}>\widehat{C}\) ; \(\widehat{ABC}>\widehat{ABH}=\widehat{D}\)
\(\Rightarrow\)\(\widehat{A}+\widehat{B}>\widehat{C}+\widehat{D}\)

Vì tứ giác ABCD có AB //CD
=> ABCD là hình thang
=> A+D = 180 độ
Mà A = 40 + D
=> 40 + D + D = 180 độ
=> 2D + 40 = 180 độ
=> 2D = 140 độ
=> D = 70 độ
=> A = 180 - 70 = 110 độ
Mà B + C = 180 độ
Mà B = 2C
=> 2C + C = 180 độ
=> 3C = 180 độ
=> C = 60 độ
=> B = 180 - 60 = 120 độ

Bài giải:
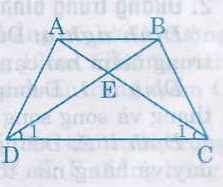
Gọi E là giao điểm của AC và BD.
∆ECD có \(\widehat{C_1}=\widehat{D}\) (do \(\widehat{ACD}=\widehat{BDC}\)) nên là tam giác cân.
Suy ra EC = ED (1)
Tương tự EA = EB (2)
Từ (1) và (2) suy ra AC = BD
Hình thang ABCD có hai đường chéo bằng nhau nên là hình thang cân.
Vì ABCD là hình thang cân nên \(\widehat A = \widehat B = {80^o}\)
Khi đó: \(\widehat C = \widehat D = \frac{{{{360}^o} - \widehat B - \widehat A}}{2} = \frac{{{{360}^o} - {{80}^o} - {{80}^o}}}{2} = {100^o}\left( {\widehat A + \widehat B + \widehat C + \widehat D = {{360}^o}} \right)\)
Chọn đáp án C