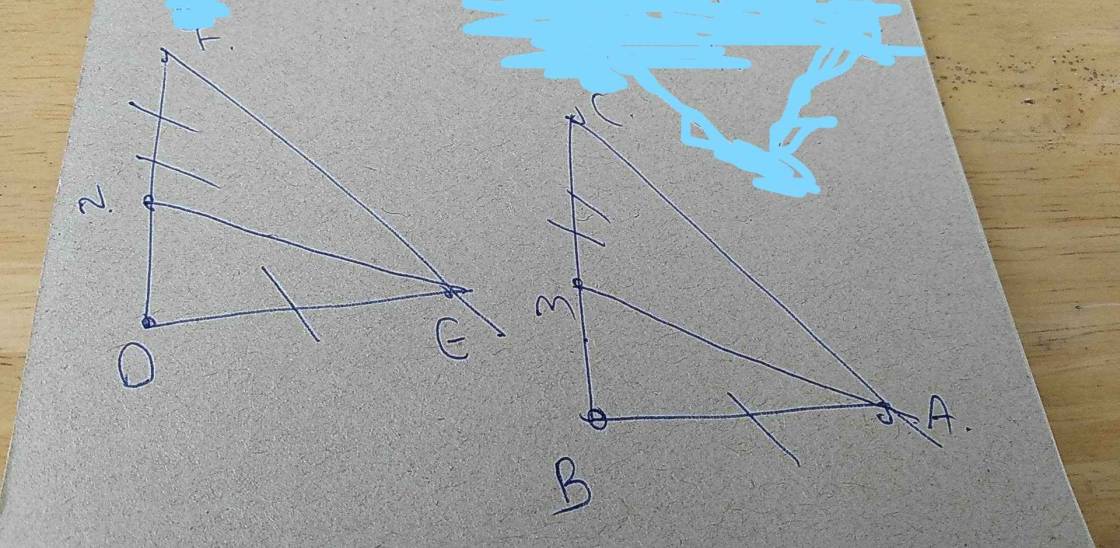
 cho mik GT,KL với ạ,( ko cần giải ạ)
cho mik GT,KL với ạ,( ko cần giải ạ)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`\text {GT | Cho đoạn thẳng BC, I là trung điểm của BC. Trên trung trực của BC lấy A (A} \ne \text {I)}`
`\text {KL |} \Delta AIB = \Delta AIC}`

| GT | ΔABC vuông tại A, BD là phân giác. DE vuông góc BC tại E AB giao DE=F |
| KL | BD là trung trực của AE |

a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
b: BA=BH
EA=EH
=>BE là trung trực của AH
c: AE=EH
EH<EC
=>AE<EC

a: Xét ΔOAH vuông tại A và ΔOBH vuông tại B có
OH chung
\(\widehat{AOH}=\widehat{BOH}\)
Do đó: ΔOAH=ΔOBH
Suy ra: OA=OB; AH=BH
b: Xét ΔBHE vuông tại B và ΔAHM vuông tại A có
HB=HA
\(\widehat{BHE}=\widehat{AHM}\)
Do đó: ΔBHE=ΔAHM
Suy ra: HE=HM
c: Ta có: OM=OE
nên O nằm trên đường trung trực của ME(1)
Ta có: HE=HM
nên H nằm trên đường trung trực của ME(2)
Từ (1) và (2) suy ra OH là đường trung trực của ME

Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40

x B A C M
a) ∆ ABC cân tại A (gt). \(\Rightarrow\) AB = AC (Tính chất tam giác cân).
Mà AB = BM (gt).
\(\Rightarrow\) AB = AC = BM.
Xét tứ giác ACMB:
BM = AC (cmt).
BM // AC (Bx // AC).
\(\Rightarrow\) Tứ giác ACBM là hình bình hành (dhnb).
Mà AB = BM (gt).
\(\Rightarrow\) Tứ giác ACBM là hình thoi (dhnb).
\(\Rightarrow\) \(AM\perp BC\) (Tính chất hình thoi).
b) Xét ∆ MBC:
MB = MC (Tứ giác ACBM là hình thoi).
\(\Rightarrow\) ∆ MBC cân tại M.

\(a,\dfrac{4}{5}\times\dfrac{7}{3}\times\dfrac{3}{4}=\dfrac{4\times7\times3}{5\times3\times4}=\dfrac{7}{5}\)
\(b,\left(\dfrac{1}{2}+\dfrac{1}{3}\right)\times\dfrac{1}{4}\)
\(=\left(\dfrac{3}{6}+\dfrac{2}{6}\right)\times\dfrac{1}{4}\)
\(=\dfrac{5}{6}\times\dfrac{1}{4}\)
\(=\dfrac{5}{24}\)
\(c,\left(\dfrac{2}{3}+\dfrac{2}{5}\right)\times\dfrac{2}{7}\)
\(=\left(\dfrac{10}{35}+\dfrac{6}{35}\right)\times\dfrac{2}{7}\)
\(=\dfrac{16}{15}\times\dfrac{2}{7}\)
\(=\dfrac{32}{105}\)
Cách `1`
`a)4/5 xx 7/3 xx 3/4`
`=28/15 xx 3/4`
`=84/60`
`=7/5`
__
`b)(1/2+1/3)xx1/4`
`=(3/6+2/6)xx1/4`
`=5/6xx1/4`
`=5/24`
__
`c)(2/3+2/5)xx2/7`
`=(10/15+6/15)xx2/7`
`=16/15xx2/7`
`=32/105`
___________________________
Cách `2`:
`a)4/5 xx 7/3 xx 3/4`
`=4/5 xx (7/3 xx 3/4)`
`=4/5 xx 7/4`
`=7/5`
__
`b)(1/2+1/3)xx1/4`
`=1/2 xx 1/4 + 1/3 xx 1/4`
`= 1/8 + 1/12`
`= 3/24+2/24`
`=5/24`
__
`c)(2/3+2/5)xx2/7`
`=2/3 xx 2/7 + 2/5 xx 2/7`
`=4/21 + 4/35`
`= 20/105+12/105`
`=32/105`
`#QiN`

a: \(Q=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)-2\sqrt{x}\left(\sqrt{x}-2\right)-5\sqrt{x}-2}{x-4}:\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)}{\left(\sqrt{x}+2\right)^2}\)
\(=\dfrac{x+3\sqrt{x}+2-2x+4\sqrt{x}-5\sqrt{x}-2}{x-4}\cdot\dfrac{\left(\sqrt{x}+2\right)^2}{\sqrt{x}\left(3-\sqrt{x}\right)}\)
\(=\dfrac{-x+2\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}\left(3-\sqrt{x}\right)}\)
\(=\dfrac{-\sqrt{x}\left(\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)\cdot\left(-1\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}-3}=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
b: Khi x=4-2căn 3 thì \(Q=\dfrac{\sqrt{3}-1+2}{\sqrt{3}-1-3}=\dfrac{\sqrt{3}+1}{\sqrt{3}-4}=\dfrac{-7-5\sqrt{3}}{13}\)
c: Q>1/6
=>Q-1/6>0
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}-3}-\dfrac{1}{6}>0\)
=>\(\dfrac{6\sqrt{x}+12-\sqrt{x}+3}{6\left(\sqrt{x}-3\right)}>0\)
=>\(\dfrac{5\sqrt{x}+9}{6\left(\sqrt{x}-3\right)}>0\)
=>căn x-3>0
=>x>9


 vẽ GT,Kl và hình ạ
vẽ GT,Kl và hình ạ




a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
=>ΔABM=ΔACM
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC