vẽ hình luôn nha! 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 1:
a) Xét \(\Delta ABC\left(\widehat{A}=90^o\right)\) có:
\(BC^2=AB^2+AC^2\) (định lí pitago)
\(\Rightarrow BC^2=8^2+6^2\)
\(\Rightarrow BC^2=64\)
\(\Rightarrow BC=8cm\)
Xét \(\Delta ABC\left(\widehat{A}=90^o\right)\) có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\)
\(\Rightarrow AH=4,8cm\)
Xét \(\Delta ABC\left(\widehat{A}=90^o\right)\) có:
\(AB^2=BH.BC\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6cm\)
\(\Rightarrow CH=BC-BH=10cm-3,6cm=6,4cm\)
b) Xét \(\Delta ABH\left(\widehat{H}=90^o\right)\) và \(\Delta ADH\left(\widehat{H}=90^o\right)\) có:
\(BH=HD\) (giả thiết)
\(AH\) là cạnh chung
\(\Rightarrow\Delta ABH=\Delta ADH\left(cgv.cgv\right)\)
\(\Rightarrow\widehat{ABH}=\widehat{ADH}\) (\(2\) cạnh tương ứng)


a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM

a: BC=5cm
b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
c: Ta có: ΔABD=ΔEBD
nên DA=DE
mà DE<DC
nên DA<DC

:a) Điện trở tương đương toàn mạch:
\(R_{12}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.40}{60+40}=24\left(\Omega\right)\)
b) Vì \(R_1//R_2\Rightarrow U=U_1=U_2=I_{12}.R_{tđ}=0,5.24=12\left(V\right)\)
Cường độ dòng điện qua mỗi điện trở:
\(I_1=\dfrac{U_1}{R_1}=\dfrac{12}{60}=0,2\left(A\right)\\ I_2=\dfrac{U_2}{R_2}=\dfrac{12}{40}=0,3\left(\Omega\right)\)
c) \(\left(R_1//R_2\right)ntR_3\)
Công suất điện R1:
\(P_1=U_1.I_1=12.0,2=2,4\left(W\right)\)
Công suất điện R3:
\(P_3=\dfrac{P_1}{2}=\dfrac{2,4}{2}=1,2\left(W\right)\)
\(R_{12}ntR_3\Rightarrow I_{12}=I_3=0,5\left(A\right)\)
Hiệu điện thế 2 đầu R3:
\(P_3=U_3.I_3\rightarrow U_3=\dfrac{P_3}{I_3}=\dfrac{1,2}{0,5}=2,4\left(V\right)\)
Điện trở R3:
\(R_3=\dfrac{U_3}{I_3}=\dfrac{2,4}{0,5}=4,8\left(\Omega\right)\)
Ko chắc :v




 đây bạn😀
đây bạn😀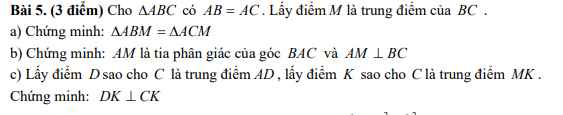
 giúp mình với,vẽ hình luôn nha(nếu dc)
giúp mình với,vẽ hình luôn nha(nếu dc)
 Vẽ hình ghi gt và kl giúp em luôn nha
Vẽ hình ghi gt và kl giúp em luôn nha
a: Xét ΔABC vuông tại A và ΔDBA vuông tại D có
góc B chung
=>ΔABC đồng dạng với ΔDBA
b: Xét ΔBDE vuông tại D và ΔBGC vuông tại G có
góc DBE chung
=>ΔBDE đồng dạng với ΔBGC
=>BD/BG=BE/BC
=>BD*BC=BG*BE
c: BF=BA
=>BF^2=BE*BG
=>BF/BE=BG/BF
=>ΔBFG đồng dạng với ΔBEF
=>góc BEF=góc BFG