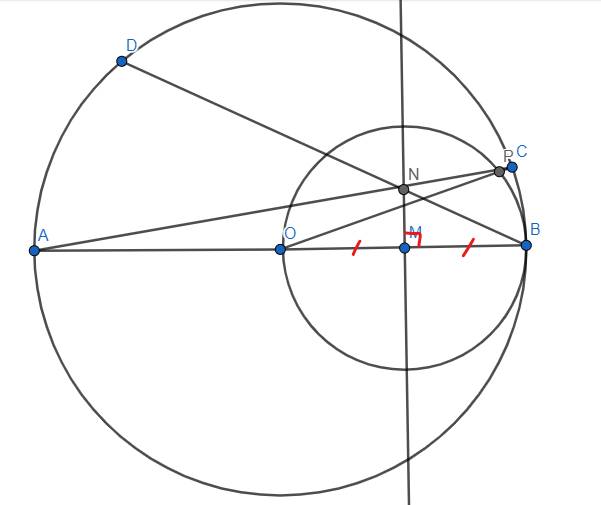
cho dtròn (O) ,đk AB ,lấy M là trung điểm OB,vẽ đtròn (M) bk MB,kẻ đthẳng d đi qua M vuông góc AB.Trên (O) lấy D ,dây BD cắt d tại N ,AN cắt (O) tại C ,đthẳng OC cắt (M) tại P :
C/m cung BC của (O) và cung BP của (M) có độ dài bằng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 5 2021
1) Vì E là giao điểm của OD và AC; AD,DC là tiếp tuyến của (O)
\(\Rightarrow OD\perp AC\)tại E
\(\Rightarrow\widehat{CEO}=90^0\)
Lại có: CH vuông góc với AB \(\Rightarrow\widehat{CHO}=90^0\)
Xét tứ giác OECH có: \(\widehat{CEO}+\widehat{CHO}=180^0\)
Mà 2 góc này ở vị trí đối nhau trong tứ giác OECH
\(\Rightarrow OECH\)nội tiếp (dhnb )
2) \(2\widehat{BCF}+\widehat{BFC}=sđ\widebat{BC}+\frac{1}{2}\left(sđ\widebat{AC}-sđ\widebat{BC}\right)\)
\(=\frac{1}{2}\left(sđ\widebat{AC}+sđ\widebat{BC}\right)\)
\(=90^0\left(đpcm\right)\)
3) Kẻ tiếp tuyến By của (O). By cắt DC tại P. Gọi K là giao điểm của BC và OP.
Ta có: AC // OP ( cùng vuông góc với BC )
Xét tam giác DOP có : EC // OP
\(\Rightarrow\frac{DE}{DO}=\frac{DC}{DP}\)(1)
Lại có: CH // BP ( cùng vuông góc với AB )
Xét tam giác DBP có: CM // BP
\(\Rightarrow\frac{DM}{DB}=\frac{DC}{DP}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\frac{DE}{DO}=\frac{DM}{DB}\)
Xét tam giác DOB có \(\frac{DE}{DO}=\frac{DM}{DB}\left(cmt\right)\); E thuộc OD , M thuộc DB
\(\Rightarrow EM//OB\)ta let đảo
Hay EM // AB ( đpcm)
8 tháng 4 2023
1:
a: M là điểm chính giữa của cung AB
=>OM vuông góc AB
góc APB=1/2*sđ cung AB=90 độ
góc COB+góc CPB=180 độ
=>COBP nội tiếp
Xet ΔAOC vuông tại O và ΔAPB vuông tại P có
góc CAO chung
=>ΔAOC đồng dạng với ΔAPB
=>AO/AP=AC/AB
=>AP*AC=AO*AB=2R^2 ko đổi
b: Xét ΔBOD vuông tại O và ΔCOA vuông tại O có
góc BDO=góc CAO
=>ΔBOD đồng dạng với ΔCOA
c: góc OPI=90 độ
=>góc IPC+góc OPC=90 độ
=>góc IPC+góc PAB=90 độ
=>góc IPC=góc ACO=góc ICP
=>IC=IP và góc IDP=góc IPD
=>IC=IP=ID
=>IC=ID
SL
28 tháng 3 2016
a> dễ có từ giác ABOC nội típ nên góc BCD=BAD
góc FIO+FCO=180 => tứ giác FIOC nội típ => IFO=ICD mà ICD=BAO => tứ giác AFOD nt => FAO=FDO
=> đpcm
4 tháng 3 2023
a: Xét (O) có
ΔBEA nội tiếp
BA là đường kính
=>ΔBEA vuông tại E
góc MCA+góc MEA=90+90=180 độ
=>MCAE nội tiếp
b: góc BFA=1/2*sđ cung BA=1/2*180=90 độ
Xét ΔBFA vuông tại F và ΔBCN vuông tai C có
góc B chung
=>ΔBFA đồng dạng với ΔBCN
=>BF/BC=BA/BN
=>BC*BA=BF*BN
Xét ΔBEA vuông tại E và ΔBCM vuông tại C có
góc EBA chung
=>ΔBEA đồng dạng với ΔBCM
=>BE/BC=BA/BM
=>BC*BA=BE*BM=BF*BN
AT
11 tháng 6 2021
a) ý bạn chắc là BD cắt đường tròn đk BC tại K nhỉ.chứ ko có điểm K
Vì BC là đường kính \(\Rightarrow\angle CKB=90\)
\(\Rightarrow\angle DHC+\angle DKC=90+90=180\Rightarrow DHCK\) nội tiếp
b) Dễ dàng chứng minh được H là trung điểm DE
\(\Rightarrow\) DE và AC cắt nhau tại trung điểm mỗi đường
\(\Rightarrow ADCE\) là hình bình hành có \(DE\bot AC\Rightarrow ADCE\) là hình thoi
\(\Rightarrow CE\parallel DA\) mà \(DA\bot DB\left(\angle ADB=90\right)\Rightarrow CE\bot DB\)
mà \(CK\bot DB\left(\angle CKB=90\right)\Rightarrow C,E,K\) thẳng hàng
c) MN cắt DE tại G.Kẻ tiếp tuyến MM' của (O)
Ta có: \(EM^2+DN^2=GM^2+GE^2+GD^2+GN^2\)
\(=\left(GM^2+GD^2\right)+\left(GE^2+GN^2\right)=MD^2+EN^2\left(1\right)\)
Vì MM' là đường kính \(\Rightarrow\angle MNM'=90\Rightarrow M'N\bot MN\)
mà \(MN\bot DE\) \(\Rightarrow M'N\parallel DE\) \(\Rightarrow DNM'E\) là hình thang
mà \(DNM'E\) nội tiếp \(\Rightarrow DNM'E\) là hình thang cân
\(\Rightarrow EN=M'D\left(2\right)\)
Từ (1) và (2) \(\Rightarrow EM^2+DN^2=DM^2+DM'^2=MM'^2=4R^2\)
độ dài cung PB=pi*MB*góc PMB/180
độ dài cung CB=pi*OB*góc COB/180
mà MB=1/2OB; góc PMB=2*góc COB
nên độ dài cung BC=độ dài cung BP