cho \(\Delta\) ABC vuông tại A, BE là phân giác( E thuộc AC)
a) CM \(\Delta\) ABE = \(\Delta\) HBE , AB = BH
b) CM \(\Delta\) ABH cân, BE là trung trực của AH
c) BA giao EH tại K , F là trung điểm KC. CM B,E,F thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Xét ΔABE và ΔHBE, ta có
:
( BE là đường phân giác BE).
BE là cạnh chung.
=> ΔABE = ΔHBE
b)
BA =BH và EA = EH (ΔABE = ΔHBE)
=> BE là đường trung trực của AH .
c)
Xét ΔKAE và ΔCHE, ta có :
(gt)
EA = EH (cmt)
( đối đỉnh).
=> ΔKAE =ΔCHE
=> EK = EC(hai cạnh tuong ứng)
d)
Xét ΔKAE vuông tại A, ta có :
KE > AE (KE là cạnh huyền)
Mà : EK = EC (cmt)
=> EC > AC.

đề ngay chỗ K là giao điểm của AB và HE là sao mk vẽ ko được???
8789

a)Vì BE là tpg của \(\widehat{ABC}\)(gt)
=>\(\widehat{ABE}\)=\(\widehat{EBH}\)(=\(\widehat{EBC}\))
Xét tam giác ABE vuông ở A và tam giác HBE vuông ở H có:
BE:cạnh chung
\(\widehat{ABE}\)=\(\widehat{EBH}\)(cmt)
=>tam giác ABE=tam giác HBE(ch-gn)
b)Vì tam giác ABE=tam giác HBE(cmt)
=>AB=HB(cặp cạnh t.ư)
Xét tam giác ABH có:AB=HB(cmt)
=>tam giác ABH cân ở B(DHNB0
Xét tam giác ABH cân ở B có:AE là tpg của \(\widehat{ABH}\)(vì AE là tpg của \(\widehat{ABC}\))
=>BE là đg trung trực của AH (t/c tam giác cân)
C) VÌ BE LÀ TIA PHÂN GIÁC CỦA ^B
=>^ABE=^EBH=60/2=30
XÉT TAM GIÁC ABC
TA CÓ ^A+^B+^C=180(Đ/L)
THAY 90+60+^C=180
^C=180-(90+60)=30
XÉT TAM GIÁC EBC
CÓ \(\widehat{C}=\widehat{B}=30\left(cmt\right)\)
=>tam EBC CÂN TẠI E (ĐPCM)
^ là góc :))
a,Xét \(\Delta\)vuông ABE và \(\Delta\)vuông HBE :
ABE^=HBE^ (gt)
BE cạnh chung
=> Tam giác ABE=tam giác HBE(ch-gn)
b,Gọi K là giao điểm của BE và AH
Xét tam giác AEK và tam giác HEK có :
EK cạnh chung
AEK^=HEK^ (cm câu a)
AE=HE (cm câu a)
=>tam giác AEK=tam giác HEK (c-g-c)
=>AKE^=EKH^=180*/2=90* ; AK=HK (1)
=>AKB^=HKB^=90* (đối đỉnh) (2)
từ 1 và 2 => BE là đg trung trực của AH
c,Ta có BAC^+ABC^+ACB^=180*
=> 90* + 60* +ACB^ = 180*
=>ACB^=30* (3)
do EBH^=30* (4)
Từ 3 và 4
=>Tam giác BEC cân tại E ( vì ACB^ = EBH^ )
D, xét tam giác vuông EHB và Tam giác vuông EHC :
EBH^=ECH^ (cm câu c)
EH cạnh chung
=>tam giác EHB = tam giác EHC (cgv-gn)
=>BH=HC
P/S : viết mỏi tay >:

Trả lời................
Tớ không biết đúng hay sai đâu nha Ý Phạm
a,Xét tam giác ABE (BAE^ vuông) và tam giác HBE (BHE^ vuông) có:
BE=BE (cạnh chung)
ABE^=HBE^
⟹ ABE^=HBE^(ch+gn)
b,Ta có:
BA=BH (tam giác ABE = tam giác HBE)
EA=EH (________________________)
⟹ BE là đường trung trực của AH
c,Xét tam giác EKA và tam giác ECH có
AE=EH (gt)
EAK^=EHK^(=90o)
AEK^=HEC^(đối đỉnh)
⟹Tam giác EKA=tam giacsEHK (g-c-g)
⟹EK=EH ( cạnh tương ứng)
d,Từ điểm E đến đường thẳng HC có:
EH là đường vuông góc
EC là đường xiên
⟹EH<EC( quan hệ đường vuông góc)
Mà EH=AE(tam giác ABE = tam giác HBE)
⟹AE<AC

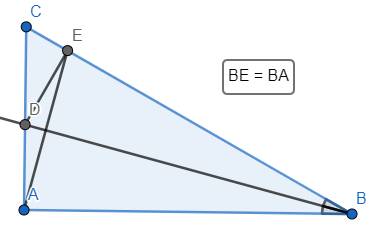
a) Xét ΔABD và ΔEBD có:
- BE = BA (giả thuyết)
- \(\widehat{ABD}=\widehat{EBD}\) (vì BD là tia phân giác của \(\widehat{ABC}\) )
- BD là cạnh chung
Suy ra ΔABD = ΔEBD (c.g.c)
b) Từ a) suy ra DE = AD (vì hai cạnh tương ứng) và \(\widehat{BAD}=\widehat{BED}=90^o\) (vì hai góc tương ứng), hay \(DE\perp BC\)
c) Từ BE = BA và DE = AD suy ra B và D đều nằm trên đường trung trực của AE, hay BD là đường trung trực của AE
a: Xet ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
=>BA=BH
b:
Xét ΔBAH có BA=BH
nên ΔBAH cân tại B
BA=BH
EA=EH
=>BE là trung trực của AH
c: Xét ΔBHK vuông tại H và ΔBAC vuông tại A có
BH=BA
góc HBK chung
=>ΔBHK=ΔBAC
=>BK=BC
=>BF là trung trực của CK(1)
Xét ΔEAK vuông tại A và ΔEHC vuông tại H có
EA=EH
góc AEK=góc HEC
=>ΔEAK=ΔEHC
=>EK=EC
=>E nằm trên trung trực của CK(2)
Từ (1), (2) suy ra B,E,F thẳng hàng