Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Xét ΔABE và ΔHBE, ta có
:
( BE là đường phân giác BE).
BE là cạnh chung.
=> ΔABE = ΔHBE
b)
BA =BH và EA = EH (ΔABE = ΔHBE)
=> BE là đường trung trực của AH .
c)
Xét ΔKAE và ΔCHE, ta có :
(gt)
EA = EH (cmt)
( đối đỉnh).
=> ΔKAE =ΔCHE
=> EK = EC(hai cạnh tuong ứng)
d)
Xét ΔKAE vuông tại A, ta có :
KE > AE (KE là cạnh huyền)
Mà : EK = EC (cmt)
=> EC > AC.

Trả lời................
Tớ không biết đúng hay sai đâu nha Ý Phạm
a,Xét tam giác ABE (BAE^ vuông) và tam giác HBE (BHE^ vuông) có:
BE=BE (cạnh chung)
ABE^=HBE^
⟹ ABE^=HBE^(ch+gn)
b,Ta có:
BA=BH (tam giác ABE = tam giác HBE)
EA=EH (________________________)
⟹ BE là đường trung trực của AH
c,Xét tam giác EKA và tam giác ECH có
AE=EH (gt)
EAK^=EHK^(=90o)
AEK^=HEC^(đối đỉnh)
⟹Tam giác EKA=tam giacsEHK (g-c-g)
⟹EK=EH ( cạnh tương ứng)
d,Từ điểm E đến đường thẳng HC có:
EH là đường vuông góc
EC là đường xiên
⟹EH<EC( quan hệ đường vuông góc)
Mà EH=AE(tam giác ABE = tam giác HBE)
⟹AE<AC

Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau

đề ngay chỗ K là giao điểm của AB và HE là sao mk vẽ ko được???
8789

a) Do tam giác ABC vuông tại A
=> Theo định lý py-ta-go ta có
BC^2=AB^2+AC^2
=>BC=\(\sqrt{AB^2+AC^2}\)= \(\sqrt{9^2+12^2}\)=\(\sqrt{225}\)=15
Vậy cạnh BC dài 15 cm
b)Xét Tam giác ABE vuông tại A và tam giác DBE vuông tại D có
BE là cạnh chung
AB=BD(Giả thiết)
=>Tam giác ABE=Tam giác DBE(CGV-CH)
B A C H D E K M
| GT | △ABC (BAC = 90o) , AB = 9 cm , AC = 12 cm D DK ⊥ BC (K AH ⊥ BC , AH ∩ BE = { M } |
KL | a, BC = ? b, △ABE = △DBE ; BE là phân giác ABC c, △AME cân |
Bài giải:
a, Xét △ABC vuông tại A có: BC2 = AB2 + AC2 = 92 + 122 = 81 + 144 = 225 => BC = 15 (cm)
b, Xét △ABE vuông tại A và △DBE vuông tại D
Có: AB = BD (gt)
BE là cạnh chung
=> △ABE = △DBE (ch-cgv)
=> ABE = DBE (2 góc tương ứng)
Mà BE nằm giữa BA, BD
=> BE là phân giác ABD
Hay BE là phân giác ABC
c, Vì △ABE = △DBE (cmt)
=> AEB = DEB (2 góc tương ứng)
Vì DK ⊥ BC (gt)
AH ⊥ BC (gt)
=> DK // AH (từ vuông góc đến song song)
=> AME = MED (2 góc so le trong)
Mà MED = MEA (cmt)
=> AME = MEA
=> △AME cân

a ) Ta có :
+) \(AB< AC\) ( gt )
\(\Rightarrow ACB< ABC\) ( quan hệ gữa góc và cạnh đối diện )
+ ) \(ABH+BAH+AHB=180\)( tổng ba góc trong một tam giác )
\(\Rightarrow ABH+60+90=180\)
\(\Rightarrow ABH=30\)
b ) Ta có :\(AD\)là phân giác góc \(A\) ( gt )
\(\Rightarrow BAD=CAD=\frac{BAC}{2}=\frac{60}{2}=30\)
Mà \(ABH=30\) ( cmt )
\(\Rightarrow ABH=BAD\)
\(\Rightarrow ABH=BAI\)
Xét tam giác \(AIB\) và tam giác \(BHA\) có :
\(AB\) chung
\(AIB=BHA=90\)
\(BAI=ABH\)
\(\Rightarrow\) tam giác \(AIB\) \(=\) tam giác \(BHA\) ( g - c - g )
c ) Xét tam giác \(ABI\) có :
\(ABI+BAI+AIB=180\)( tổng ba góc trong một tam giác )
\(\Rightarrow ABI+30+90=180\)
\(\Rightarrow ABI=60\)
\(\Rightarrow ABE=60\) ( 1 )
Xét tam giác \(ABE\) có :
\(ABE+BAE+AEB=180\) ( tổng ba góc trong một tam giác )
\(\Rightarrow60+60+AEB=180\)
\(\Rightarrow AEB=60\) ( 2 )
Mà \(BAE=60\) ( gt ) ( 3 )
Từ ( 1 ) ; ( 2 ) ; ( 3 )
\(\Rightarrow\) tam giác \(ABE\) đều
Chứng minh câu d:
A B C D H E I 1
Ta có: AE = AB < AC
=> E thuộc canh AC
\(\Delta\)ABE đều mà AD vuông BE tại I => AD là đường trung trực của DE => DB = DE (1)
Dễ chứng minh \(\Delta\)ABD = \(\Delta\)AED
=> ^ABD = ^AED => ^B1 = ^DEC ( góc ngoài )
mà ^B1 là góc ngoài của \(\Delta\)ABC tại B => ^B1 > ^C
=> ^DEC > ^C = ^ECD
Xét trong \(\Delta\)DEC có: ^DEC > ^ECD => DC > DE (2)
Từ (1); (2) => DC > DB

a.Xét △ABE vuông tại A và △HBE vuông tại H có :
BE chung
góc ABE = góc HBE (vì BE là tia phân giác)
=>△ABE = △HBE (cạnh huyền - góc nhọn)
b. Vì △ABE = △HBE (chứng minh trên)
=>AB = HB (2 cạnh tương ứng)
=> △AHB cân tại B
mà BE là tia phân giác của góc ABC (giả thuyết)
nên BE đồng thời là đường trung trực của đoạn thẳng AH.
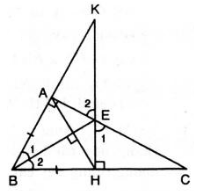


 BC : BD = BA.
BC : BD = BA.
a)Vì BE là tpg của \(\widehat{ABC}\)(gt)
=>\(\widehat{ABE}\)=\(\widehat{EBH}\)(=\(\widehat{EBC}\))
Xét tam giác ABE vuông ở A và tam giác HBE vuông ở H có:
BE:cạnh chung
\(\widehat{ABE}\)=\(\widehat{EBH}\)(cmt)
=>tam giác ABE=tam giác HBE(ch-gn)
b)Vì tam giác ABE=tam giác HBE(cmt)
=>AB=HB(cặp cạnh t.ư)
Xét tam giác ABH có:AB=HB(cmt)
=>tam giác ABH cân ở B(DHNB0
Xét tam giác ABH cân ở B có:AE là tpg của \(\widehat{ABH}\)(vì AE là tpg của \(\widehat{ABC}\))
=>BE là đg trung trực của AH (t/c tam giác cân)
C) VÌ BE LÀ TIA PHÂN GIÁC CỦA ^B
=>^ABE=^EBH=60/2=30
XÉT TAM GIÁC ABC
TA CÓ ^A+^B+^C=180(Đ/L)
THAY 90+60+^C=180
^C=180-(90+60)=30
XÉT TAM GIÁC EBC
CÓ \(\widehat{C}=\widehat{B}=30\left(cmt\right)\)
=>tam EBC CÂN TẠI E (ĐPCM)
^ là góc :))
a,Xét \(\Delta\)vuông ABE và \(\Delta\)vuông HBE :
ABE^=HBE^ (gt)
BE cạnh chung
=> Tam giác ABE=tam giác HBE(ch-gn)
b,Gọi K là giao điểm của BE và AH
Xét tam giác AEK và tam giác HEK có :
EK cạnh chung
AEK^=HEK^ (cm câu a)
AE=HE (cm câu a)
=>tam giác AEK=tam giác HEK (c-g-c)
=>AKE^=EKH^=180*/2=90* ; AK=HK (1)
=>AKB^=HKB^=90* (đối đỉnh) (2)
từ 1 và 2 => BE là đg trung trực của AH
c,Ta có BAC^+ABC^+ACB^=180*
=> 90* + 60* +ACB^ = 180*
=>ACB^=30* (3)
do EBH^=30* (4)
Từ 3 và 4
=>Tam giác BEC cân tại E ( vì ACB^ = EBH^ )
D, xét tam giác vuông EHB và Tam giác vuông EHC :
EBH^=ECH^ (cm câu c)
EH cạnh chung
=>tam giác EHB = tam giác EHC (cgv-gn)
=>BH=HC
P/S : viết mỏi tay >: