Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét ΔHAB vuông tại H và ΔBAE vuông tại B có
\(\widehat{BAH}\) chung
Do đó: ΔHAB\(\sim\)ΔBAE(g-g)
xét tam giác ABC và tam giác HBA có
góc BAC=góc AHB=90 độ
góc B chung
suy ra tam giác ABC đồng dạng với tam giác HBA
suy ra AB phần HB = BC phần AB
a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
Suy ra: \(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)(Các cặp cạnh tuong ứng tỉ lệ)
hay \(AB^2=BH\cdot BC\)(đpcm)
b) Xét ΔCHA vuông tại H và ΔAHB vuông tại H có
\(\widehat{HAC}=\widehat{HBA}\left(=90^0-\widehat{C}\right)\)
Do đó: ΔCHA\(\sim\)ΔAHB(g-g)
Suy ra: \(\dfrac{CA}{AB}=\dfrac{HA}{HB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AC}{HA}=\dfrac{AB}{BH}\)(1)
Xét ΔHBA có BI là đường phân giác ứng với cạnh AH(gt)
nên \(\dfrac{IA}{IH}=\dfrac{AB}{BH}\)(2)
Từ (1) và (2) suy ra \(\dfrac{IA}{IH}=\dfrac{AC}{HA}\)(3)
c) Xét ΔAHC có AK là đường phân giác ứng với cạnh CH(gt)
nên \(\dfrac{CK}{KH}=\dfrac{AC}{HA}\)(4)
Từ (3) và (4) suy ra \(\dfrac{CK}{KH}=\dfrac{AI}{IH}\)
hay KI//AC(Định lí Ta lét đảo)
a: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
BE là phân giác
=>AE/AB=CE/BC
=>AE/3=CE/5=16/8=2
=>AE=6cm; CE=10cm
b: Xet ΔHAB vuông tại H và ΔHCA vuông tại H có
góc HAB=góc HCA
=>ΔHAB đồng dạng vơi ΔHCA
c: ΔABC vuông tại A
mà AH là đường cao
nên BA^2=BH*BC
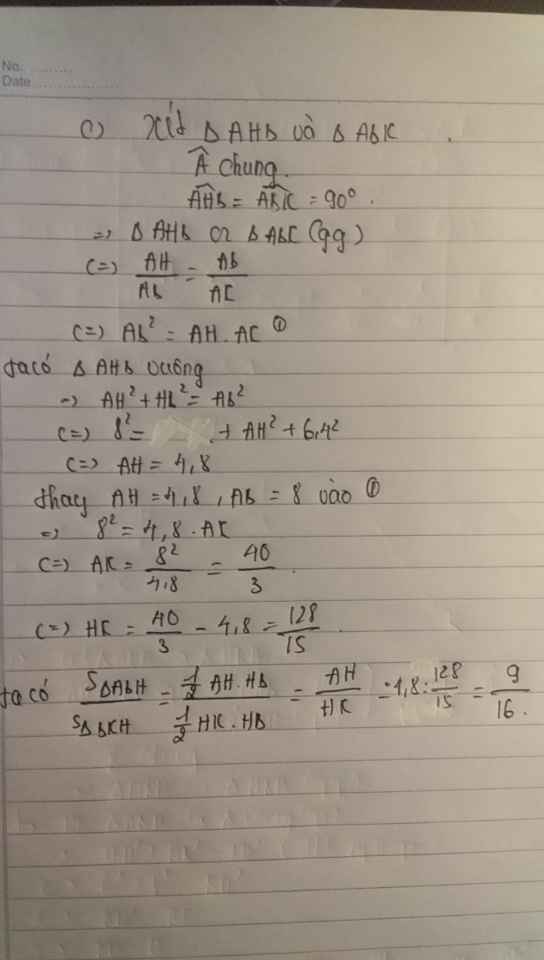
a: Xét ΔHAB vuông tại H và ΔBAE vuông tại B có
góc HAB chung
=>ΔHAB đồng dạng với ΔBAE
=>AH/AB=AB/AE
=>AB^2=AH*AE
b: Xet ΔHBE vuông tại H và ΔHAB vuông tại H có
góc HBE=góc HAB
Do đo: ΔHBE đồng dạngvới ΔHAB
=>HB/HA=HE/HB
=>HB^2=HE*HA