Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔHAB vuông tại H và ΔBAE vuông tại B có
góc HAB chung
=>ΔHAB đồng dạng với ΔBAE
=>AH/AB=AB/AE
=>AB^2=AH*AE
b: Xet ΔHBE vuông tại H và ΔHAB vuông tại H có
góc HBE=góc HAB
Do đo: ΔHBE đồng dạngvới ΔHAB
=>HB/HA=HE/HB
=>HB^2=HE*HA

a, Xét tg HBA và tgABC:
Có: góc B chung
H=A=90
=> tg HBA đồng dạng ABC (gg)
b, Vì tg BHA đồng dạng tg ABC:
=>AB/HB=BC/AB
=>đpcm.
c, Áp dụng tính chất tia phân giác:
=>AB/AC=BI/IC=>BI/AB=IC/AC
Áp dụng tính chất dãy tỉ số bằng nhau:
BI/AB=IC/AC=BI+IC/AB+AC=BC/AB+AC=10/6+8=5/7
Suy ra: BI=5/7.6=4,3
IC=5/7.8=5,7
Nhớ k nha.

A B C H
\(\text{Xét tam giác ABC và tam giác HBA,có:}\)
\(\widehat{A}=\widehat{H}=90^0\)
\(\widehat{B}\)\(\text{chung}\)
\(\text{Vậy tam giác ABC~tam giác HBA(g.g) }\)
\(\Rightarrow\frac{AB}{HB}=\frac{BC}{AB}\Rightarrow AB^2=HB.BC\)
B.cHỨNG MINH TƯƠNG TỰ
b) xét tam giác HAB và tam giác HCA ,có:
góc BHA = góc CHA (=90)
góc BAH = góc HCA (cùng phụ B)
nên tam giác HAB ~ tam giác HCA
=> HA/HB = HC/HA
=> HA2 = HC.HB

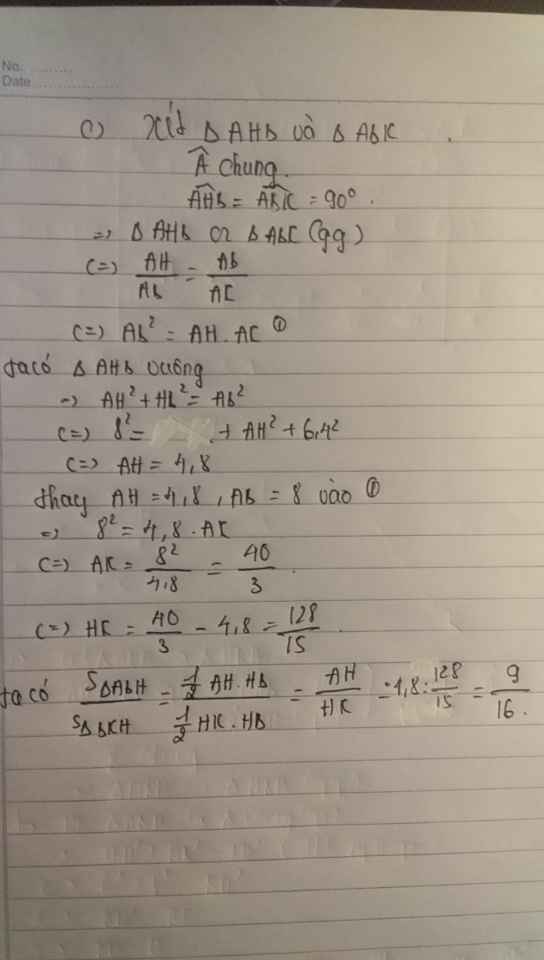
a) Xét ΔHAB vuông tại H và ΔBAE vuông tại B có
\(\widehat{BAH}\) chung
Do đó: ΔHAB\(\sim\)ΔBAE(g-g)