Giải phương trình :
(2x+1)(x+1)²(2x+3)=1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{2x-3}{x-1}< \dfrac{1}{3}\left(đk:x\ne1\right)\)
\(\Leftrightarrow6x-9< x-1\Leftrightarrow5x< 8\Leftrightarrow x< \dfrac{8}{5}\) và ĐK \(x\ne1\)
\(\dfrac{2x-3}{x-1}>\dfrac{1}{3}\left(đk:x\ne1\right)\)
\(\Leftrightarrow x-1< 6x-9\Leftrightarrow5x>8\Leftrightarrow x>\dfrac{8}{5}\) và ĐK \(x\ne1\)

\(\dfrac{x}{2x-6}-\dfrac{x}{2x+2}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\left(ĐKXĐ:x\ne-1,x\ne3\right)\)
\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}-\dfrac{x}{2\left(x+1\right)}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\)
\(\Leftrightarrow\dfrac{x\left(x+1\right)}{2\left(x+1\right)\left(x-3\right)}-\dfrac{x\left(x-3\right)}{2\left(x+1\right)\left(x-3\right)}=\dfrac{2x\cdot2}{2\left(x+1\right)\left(x-3\right)}\)
\(\Rightarrow x\left(x+1\right)-x\left(x-3\right)=4x\)
\(\Leftrightarrow x^2+x-x^2+3x=4x\)
\(\Leftrightarrow x^2+x-x^2+3x-4x=0\)
\(\Leftrightarrow0x=0\)
Phương trình có vô số nghiệm , trừ x = -1,x = 3
Vậy ...
\(\dfrac{12x+1}{12}< \dfrac{9x+1}{3}-\dfrac{8x+1}{4}\)
\(\Leftrightarrow12\cdot\dfrac{12x+1}{12}< 12\cdot\dfrac{9x+1}{3}-12\cdot\dfrac{8x+1}{4}\)
\(\Leftrightarrow12x+1< 4\left(9x+1\right)-3\left(8x+1\right)\)
\(\Leftrightarrow12x+1< 36x+4-24x-3\)
\(\Leftrightarrow12x+1< 12x+1\)
\(\Leftrightarrow12x-12x< 1-1\)
\(\Leftrightarrow0x< 0\)
Vậy S = {x | x \(\in R\)}

a) |3x| = x + 6 (1)
Ta có 3x = 3x khi x ≥ 0 và 3x = -3x khi x < 0
Vậy để giải phương trình (1) ta quy về giải hai phương trình sau:
+ ) Phương trình 3x = x + 6 với điều kiện x ≥ 0
Ta có: 3x = x + 6 ⇔ 2x = 6 ⇔ x = 3 (TMĐK)
Do đó x = 3 là nghiệm của phương trình (1).
+ ) Phương trình -3x = x + 6 với điều kiện x < 0
Ta có -3x = x + 6 ⇔ -4x + 6 ⇔ x = -3/2 (TMĐK)
Do đó x = -3/2 là nghiệm của phương trình (1).
Vậy tập nghiệm của phương trình đã cho S = {3; -3/2}
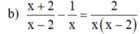
ĐKXĐ: x ≠ 0, x ≠ 2
Quy đồng mẫu hai vễ của phương trình, ta được:
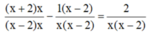
![]()
![]()
![]()
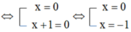
![]()
Vậy tập nghiệm của phương trình là S = {-1}
c) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)
⇔ 2x2 – 2x + 2x – 2 – 3 > –5x – (6x – 2x2 + 3 – x)
⇔ 2x2 – 5 ≥ –5x – 6x + 2x2 – 3 + x
⇔ 10x ≥ 2 ⇔ x ≥ 1/5
Tập nghiệm: S = {x | x ≥ 1/5}

Lời giải:
ĐKXĐ: $x\neq 0; \frac{-3}{2}; \frac{-1}{2}; -3$
PT $\Leftrightarrow (\frac{1}{x}-\frac{3}{2x+1})+(\frac{5}{2x+3}-\frac{4}{x+3})=0$
$\Leftrightarrow \frac{1-x}{x(2x+1)}+\frac{3-3x}{(2x+3)(x+3)}=0$
$\Leftrightarrow \frac{1-x}{x(2x+1)}+\frac{3(1-x)}{(2x+3)(x+3)}=0$
$\Leftrightarrow (1-x)\left[\frac{1}{x(2x+1)}+\frac{3}{(2x+3)(x+3)}\right]=0$
TH1: $1-x=0\Leftrightarrow x=1$ (tm)
TH2: $\frac{1}{x(2x+1)}+\frac{3}{(2x+3)(x+3)}=0$
$\Rightarrow (2x+3)(x+3)+3x(2x+1)=0$
$\Leftrightarrow 8x^2+12x+9=0$
$\Leftrightarrow (2x+3)^2+4x^2=0$
$\Rightarrow (2x+3)^2=x^2=0$ (vô lý)
Do đó $x=1$ là nghiệm duy nhất.

a: \(3+\sqrt{2x-3}=x\)
=>\(\sqrt{2x-3}=x-3\)
=>x>=3 và 2x-3=(x-3)^2
=>x>=3 và x^2-6x+9=2x-3
=>x>=3 và x^2-8x+12=0
=>x>=3 và (x-2)(x-6)=0
=>x>=3 và \(x\in\left\{2;6\right\}\)
=>x=6
b: \(\left(\sqrt{x}+1\right)\left(2\sqrt{x}-3\right)-2x=-4\)
=>\(2x-3\sqrt{x}+2\sqrt{x}-3-2x=-4\)
=>\(-\sqrt{x}-3=-4\)
=>\(-\sqrt{x}=-1\)
=>căn x=1
=>x=1(nhận)
c: \(\sqrt{2x+1}-x+1=0\)
=>\(\sqrt{2x+1}=x-1\)
=>x>=1 và (x-1)^2=2x+1
=>x>=1 và x^2-2x+1=2x+1
=>x>=1 và x^2-4x=0
=>x(x-4)=0 và x>=1
=>x=4


a: =>|x-3/2|=2
\(\Leftrightarrow x-\dfrac{3}{2}\in\left\{2;-2\right\}\)
hay \(x\in\left\{\dfrac{7}{2};-\dfrac{1}{2}\right\}\)
f: \(\Leftrightarrow\left[{}\begin{matrix}2x+3=x-2\\2x+3=2-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-\dfrac{1}{3}\end{matrix}\right.\)


\(\left(2x-1\right)\left(2x-3\right)\left(x+1\right)^2=18\)
\(\Leftrightarrow\left(2x-1\right)\left(2x-3\right)\left(2x+2\right)^2=72\) (*)
Đặt \(a=2x+2\)
(*) \(\Leftrightarrow\left(a-3\right)\left(a-5\right).a^2=0\)
\(\Leftrightarrow\left(a^3-5a^2\right)\left(a-3\right)=0\)
\(\Leftrightarrow a^4-8a^3+15a^2=0\)
\(\Leftrightarrow a^4-5a^3-3a^3+15a^2=0\)
\(\Leftrightarrow a^3.\left(a-5\right)-3a^2.\left(a-5\right)=0\)
\(\Leftrightarrow\left(a-5\right)\left(a-3\right).a^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\2x-1=0\\\left(2x+2\right)^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{1}{2}\\x=-1\end{matrix}\right.\)
\(\left(2x+1\right)\left(x+1\right)^2\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=0\\\left(x+1\right)^2=0\\2x+3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-1\\x^2+2x+1=0\\2x=-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Vậy \(S=\left\{-\dfrac{1}{2};-1;-\dfrac{3}{2}\right\}\)