Chứng minh góc ACD=ACB, biết AB=AD, góc ABC=ADC=90°
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét hai tam giác vuông ABC và ADC có: AB = AD, AC chung.
Nên \(\Delta ABC = \Delta ADC\) (cạnh huyền - cạnh góc vuông) nên \(\widehat {ACB} = \widehat {ACD}\) (2 góc tương ứng)


a) Xét tam giác \(ADC\)vuông tại \(D\):
\(tan\widehat{ACD}=\frac{AD}{DC}=\frac{1}{2}\Rightarrow\widehat{ACD}=arctan\frac{1}{2}\)
b) Xét tam giác \(ADC\)vuông tại \(D\):
\(AC^2=AD^2+DC^2=AD^2+4AD^2=5AD^2\)
\(\Leftrightarrow AD=\sqrt{\frac{AC^2}{5}}=\sqrt{\frac{25^2}{5}}=5\sqrt{5}\left(cm\right)\)
\(AB=AD=5\sqrt{5}\left(cm\right),CD=2AD=10\sqrt{5}\left(cm\right)\).
c) Xét tam giác \(ADC\)vuông tại \(D\):
\(DH=\frac{AD.DC}{AC}=\frac{10\sqrt{5}.5\sqrt{5}}{25}=10\left(cm\right)\)
\(AH=\frac{AD^2}{AC}=\frac{AB^2}{AC}\Leftrightarrow\frac{AB}{AC}=\frac{AH}{AB}\)
Xét tam giác \(ABH\)và tam giác \(ACB\):
\(\widehat{A}\)chung
\(\frac{AB}{AC}=\frac{AH}{AB}\)
suy ra \(\Delta ABH~\Delta ACB\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABH}=\widehat{ACB}\)
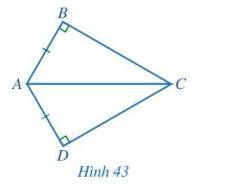
\(\Delta ABC\), \(\Delta ADC\)
AB = AD
\(\widehat{ABC}\) = \(\widehat{ADC}\) = 90o
Vì ΔABC có \(\widehat{ABC}\)=90o (gt) nên ∆ABC vuông tại B.
Vì ∆ADC có \(\widehat{ADC}\)=90° (gt) nên ∆ADC vuông tại D.
Xét hai tam giác ABC (vuông tại B) và tam giác ADC (vuông tại D) có:
AC là cạnh chung
AB = AD (gt)
Suy ra Δ∆ABC = ∆ADC (cạnh huyền – cạnh góc vuông)
Do đó \(\widehat{ACB}\)=\(\widehat{ADC}\) (hai góc tương ứng)
Vậy \(\widehat{ACB}=\widehat{ACD}\)