K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
Xét hai tam giác vuông ABC và ADC có: AB = AD, AC chung.
Nên \(\Delta ABC = \Delta ADC\) (cạnh huyền - cạnh góc vuông) nên \(\widehat {ACB} = \widehat {ACD}\) (2 góc tương ứng)

14 tháng 7 2017
a) Xét 2 tam giác ABD và ADC có :
AB = AC (gt)
Góc BAD = Góc DAC
AD chung
=> : BAD = ADC (c.g.c). Vậy Góc ABC = Góc ACB.
b) Từ chứng minh trên ta có : Góc ADC = Góc ADB. Mà 2 góc đó lại kề bù với nhau : => Góc ADC = Góc ADB = 90 độ
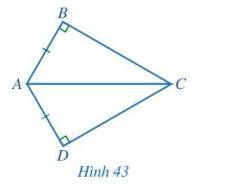
\(\Delta ABC\), \(\Delta ADC\)
AB = AD
\(\widehat{ABC}\) = \(\widehat{ADC}\) = 90o
Vì ΔABC có \(\widehat{ABC}\)=90o (gt) nên ∆ABC vuông tại B.
Vì ∆ADC có \(\widehat{ADC}\)=90° (gt) nên ∆ADC vuông tại D.
Xét hai tam giác ABC (vuông tại B) và tam giác ADC (vuông tại D) có:
AC là cạnh chung
AB = AD (gt)
Suy ra Δ∆ABC = ∆ADC (cạnh huyền – cạnh góc vuông)
Do đó \(\widehat{ACB}\)=\(\widehat{ADC}\) (hai góc tương ứng)
Vậy \(\widehat{ACB}=\widehat{ACD}\)