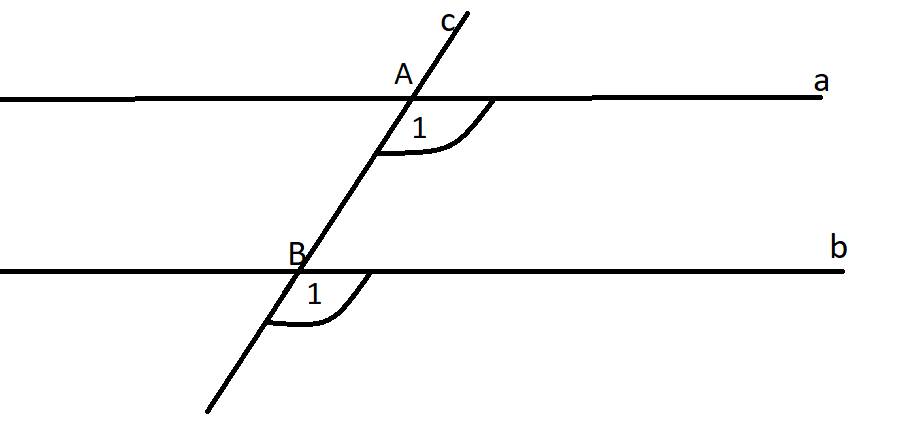
Quan sát hình vẽ và chứng minh a\(//\)b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
1
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
Vì \(\left\{ \begin{array}{l}BC \bot AB'\\B'C' \bot AB'\end{array} \right. \Rightarrow BC//B'C'\)(quan hệ từ vuông góc đến song song).
- Xét tam giác \(AB'C'\) có \(BC//B'C'\) và \(BC\) cắt \(AB';AC'\) lần lượt tại \(B;C\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{AB}}{{AB'}} = \frac{{BC}}{{B'C'}} \Rightarrow \frac{x}{{x + h}} = \frac{a}{{a'}} \Rightarrow xa' = a\left( {x + h} \right) \Leftrightarrow xa' = ax + ah\)
\( \Leftrightarrow xa' - ax = ah \Leftrightarrow x\left( {a' - a} \right) = ah \Leftrightarrow x = \frac{{ah}}{{a' - a}}\) (điều phải chứng minh).
CM
27 tháng 1 2019
a) Ta có: OA = OB (= bán kính đường tròn (O))
O’A = O’B (= bán kính đường tròn (O’))
⇒ OO’ là đường trung trực của AB
b) Hình 86a) Hai đường tròn tiếp xúc ngoài thì A nằm giữa O và O’
Hình 86b) Hai đường tròn tiếp xúc trong thì A nằm ngoài đoạn OO’
QT
1
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Xét tam giác \(A'B'C'\) ta có:
\(\widehat {A'} + \widehat {B'} + \widehat {C'} = 180^\circ \)
Thay số: \(79^\circ + \widehat {B'} + 41^\circ = 180^\circ \)
\( \Rightarrow \widehat {B'} = 180^\circ - 79^\circ - 41^\circ = 60^\circ \)
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) ta có:
\(\widehat A = \widehat {A'} = 79^\circ \) (giả thuyết)
\(\widehat B = \widehat {B'} = 60^\circ \) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta A'B'C'\) (g.g)
b) Vì \(\Delta ABC\backsim\Delta A'B'C'\) nên \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) (các cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{4}{6} = \frac{6}{{B'C'}} \Rightarrow B'C' = \frac{{6.6}}{4} = 9\)
Vậy \(B'C' = 9\).
14 tháng 9 2023
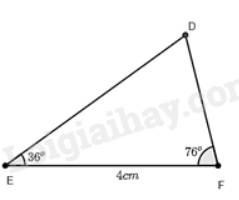
a) Xét tam giác \(DEF\) và tam giác \(AMC\) có:
\(\widehat E = \widehat M = 36^\circ \)
\(\widehat F = \widehat C = 76^\circ \) (chứng minh trên)
Suy ra, \(\Delta DEF\backsim\Delta AMC\) (g.g).
b) Đổi 25m = 2500 cm.
Dùng thước đo độ dài cạnh \(DF\) ta được độ dài \(DF\) là 2,6cm.
Vì \(\Delta DEF\backsim\Delta AMC\) nên \(\frac{{DF}}{{EF}} = \frac{{AC}}{{MC}}\) (hai cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{2,6}}{4} = \frac{{AC}}{{2500}} \Rightarrow AC = \frac{{2,6.2500}}{4} = 1625\).
Vậy khoảng cách giữa hai điểm \(A\) và \(C\) là 1625 cm hay 16,25m.
NV
Nguyễn Việt Dũng
CTVVIP
2 tháng 8 2023
Tham khảo:
- Về kinh tế:
+ Thành phố Hồ Chí Minh có đóng góp nhiều nhất vào tổng thu ngân sách nhà nước, đứng đầu cả nước về phát triển dịch vụ và công nghiệp.
+ Thành phố Hồ Chí Minh có giá trị sản xuất công nghiệp đứng đầu cả nước với các ngành chủ yếu như: điện tử - tin học, thực phẩm- đồ uống, cơ khí, dệt may, da giày....
- Về văn hóa:
+ Thành phố Hồ Chí Minh là nơi có nhiều di tích lịch sử và bảo tàng như: Bến cảng Nhà Rồng Nhà thờ Đức Bà, chợ Bến Thành, Địa đạo Củ Chi, Dinh Độc Lập, Bảo tàng Mĩ thuật, Bảo tàng Chứng tích chiến tranh,...
+ Thành phố Hồ Chí Minh là nơi hội tụ cư dân từ khắp nơi, góp phần tạo sự đa dạng về văn hóa.
- Về giáo dục: Thành phố Hồ Chí Minh có nhiều viện nghiên cứu, trường đại học, trung tâm khoa học - công nghệ thuộc các lĩnh vực khác nhau, làm nòng cốt cho sự phát triển giáo dục của vùng, đáp ứng nhu cầu phát triển kinh tế - xã hội của đất nước.
HQ
Hà Quang Minh
Giáo viên
7 tháng 10 2023
1. Các góc có đỉnh A trong hình vẽ : \(\widehat {DAC};\widehat {DAB};\widehat{BAC}.\)
Các góc có đỉnh B trong hình vẽ : \(\widehat {ABC};\widehat {ABD};\widehat {DBC}\).
2.
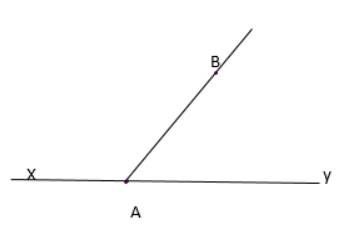
a. Các góc có trong hình vẽ là :
\(\widehat{xAB} ; \widehat{BAy} ; \widehat{xAy}\)
b. Ax và Ay là hai tia đối nhau nên \(\widehat{xAy}\) là góc bẹt.
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\) (1)
Vì \(AKCH\) là hình bình hành (gt)
Mà \(O\) là trung điểm của \(AC\)
Suy ra \(O\) là trung điểm của \(HK\)
Ta thấy $\widehat{A_1} = \widehat{B_1}$ mà hai góc này ở vị trí đồng vị nên $a$ // $b$.