Cho tam giác abc có góc acb =40 độ ,đường cao ah .Tia phân giác của góc hac cắt bc tại d
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 6 2023
a: Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
góc HAD=góc KAD
=>ΔAHD=ΔAKD
b: AH=AK
DH=DK
=>AD là trung trực của HK
c: Gọi M là giao của DK với AH
Xét ΔAMC có
MK,CH là đường cao
MK cắt CH tại D
=>D là trực tâm
=>AD vuông góc MC
mà AD vuông góc CE
nên C,M,E thẳng hàng
=>AH,KD,CE đồng quy tại M
NC
11 tháng 3 2021
Tam giác ABC có: góc A = 90 *
=> góc BAD + góc DAC=90*
Tam giác AHD có : góc AHD = 90*
=> góc HDA + góc HAD = 90*
mà góc DAC = góc HAD ( do AD là pg góc HAC)
=> Góc BAD = góc HDA
=> Tam giác ABD cân tại B => AB = BD
Mặt khác : c/m đc Tam giác ABH đồng dạng với tam giác CBA
=> AB ^ 2 = BH x BC
= ( BD -12) BC = (AB - 12).50
= 50AB - 600
<=> AB^2 - 50AB + 600 = 0
Cre:mạng
CM
21 tháng 7 2017
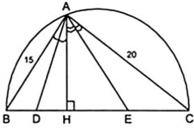
Áp dụng định lý Py – ta – go vào tam giác ABC vuông tại A, ta được:
B C 2 = A C + A B 2 ⇒ B C 2 = 15 2 + 20 2 ⇔ B C 2 = 25 2 ⇔ BC = 25( cm )
Đặt BD = x ⇒ DC = 25 - x
Áp dụng định lý Py 0 ta – go vào hai tam giác vuông AHB và AHC, ta được:
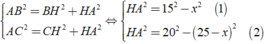
Trừ theo vế các đẳng thức ( 1 ) và ( 2 ) ta được:
15 2 - x 2 - 20 2 + ( 25 - x ) 2 = 0 ⇔ 50x = 450 ⇔ x = 9( cm )
Nên HC = 25 - 9 = 16( cm )
Thay x = 9 vào đẳng thức ( 1 ) ta có: H A 2 = 15 2 - 9 2 = 122 ⇔ HA = 12( cm )
Áp dụng tính chất đường phân giác AD vào tam giác AHB, ta được:
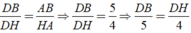
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
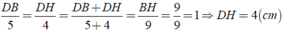
Áp dụng tính chất đường chất đường phân giác AE của tam giác ACH, ta được:
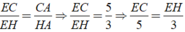
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
18 tháng 2 2022
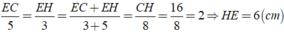
a: \(\widehat{DAE}=\dfrac{1}{2}\left(\widehat{HAB}+\widehat{HAC}\right)=\dfrac{1}{2}\cdot90^0=45^0\)
b: Xét ΔAEH và ΔAEF có
AE chung
\(\widehat{HAE}=\widehat{FAE}\)
AH=AF
Do đó: ΔAEH=ΔAEF
c: Ta có: ΔAEH=ΔAEF
nên \(\widehat{AHE}=\widehat{AFE}=90^0\)
=>EF⊥AC
mà AC⊥AB
nên EF//AB
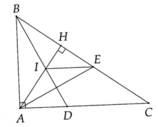
Bài 3:
a) Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)(AD là tia phân giác của \(\widehat{HAK}\))
Do đó: ΔAHD=ΔAKD(Cạnh huyền-góc nhọn)
b)Ta có: ΔAHD=ΔAKD(cmt)
nên AH=AK(hai cạnh tương ứng) và DH=DK(hai cạnh tương ứng)
Ta có: AH=AK(cmt)
nên A nằm trên đường trung trực của HK(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: DH=DK(cmt)
nên D nằm trên đường trung trực của HK(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AD là đường trung trực của HK
hay AD\(\perp\)HK(đpcm)