K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

28 tháng 6 2023
a: Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
góc HAD=góc KAD
=>ΔAHD=ΔAKD
b: AH=AK
DH=DK
=>AD là trung trực của HK
c: Gọi M là giao của DK với AH
Xét ΔAMC có
MK,CH là đường cao
MK cắt CH tại D
=>D là trực tâm
=>AD vuông góc MC
mà AD vuông góc CE
nên C,M,E thẳng hàng
=>AH,KD,CE đồng quy tại M

18 tháng 2 2022
a: \(\widehat{DAE}=\dfrac{1}{2}\left(\widehat{HAB}+\widehat{HAC}\right)=\dfrac{1}{2}\cdot90^0=45^0\)
b: Xét ΔAEH và ΔAEF có
AE chung
\(\widehat{HAE}=\widehat{FAE}\)
AH=AF
Do đó: ΔAEH=ΔAEF
c: Ta có: ΔAEH=ΔAEF
nên \(\widehat{AHE}=\widehat{AFE}=90^0\)
=>EF⊥AC
mà AC⊥AB
nên EF//AB

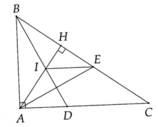


Bài 3:
a) Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)(AD là tia phân giác của \(\widehat{HAK}\))
Do đó: ΔAHD=ΔAKD(Cạnh huyền-góc nhọn)
b)Ta có: ΔAHD=ΔAKD(cmt)
nên AH=AK(hai cạnh tương ứng) và DH=DK(hai cạnh tương ứng)
Ta có: AH=AK(cmt)
nên A nằm trên đường trung trực của HK(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: DH=DK(cmt)
nên D nằm trên đường trung trực của HK(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AD là đường trung trực của HK
hay AD\(\perp\)HK(đpcm)